题目内容
已知sin（
-x）=
，则cos（
π-x）=（ ）
| π |
| 5 |
| 3 |
| 5 |
| 7 |
| 10 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
考点：两角和与差的余弦函数,运用诱导公式化简求值
专题：三角函数的求值
分析：由条件利用诱导公式可得cos（
+x）=
，再利用诱导公式化简所给式子，可得结果．
| 3π |
| 10 |
| 3 |
| 5 |
解答：
解：∵已知sin（
-x）=
，∴cos[
-（
-x）]=cos（
+x）=sin（
-x）=
，
则cos（
π-x）=-cos[π-（
+x）]=-cos（
+x）=-
，
故选：C．
| π |
| 5 |
| 3 |
| 5 |
| π |
| 2 |
| π |
| 5 |
| 3π |
| 10 |
| π |
| 5 |
| 3 |
| 5 |
则cos（
| 7 |
| 10 |
| 3π |
| 10 |
| 3π |
| 10 |
| 3 |
| 5 |
故选：C．
点评：本题主要考查应用诱导公式化简三角函数式，要特别注意符号的选取，这是解题的易错点，属于基础题．
练习册系列答案
相关题目
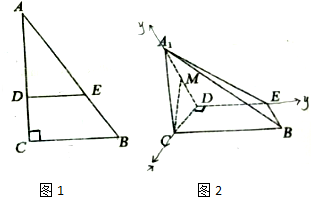如图1，在Rt△ABC中，∠C=90°，BC=3，AC=6，DE分别为AC、AB上的点，且DE∥BC，DE=2，将△ADE沿DE折起到△A1DE的位置，使A1C⊥CD，如图2．求证：A1C⊥平面BCDE．