题目内容
在△ABN中，点P在BN上，若
=m
+n
，证明：m+n=1．
| AP |
| AB |
| AN |
考点：向量的共线定理
专题：平面向量及应用
分析：由B，P，N三点共线，利用向量共线定理可得存在实数λ使得
=λ
，化简整理，与
=m
+n
，比较，利用平面向量共线定理即可得出．
| BP |
| BN |
| AP |
| AB |
| AN |
解答：
证明：如图所示，
∵B，P，N三点共线，
∴存在实数λ使得
=λ
，
∴
-
=λ
-λ
，
∴
=λ
+(1-λ)
，
又
=m
+n
，
∴m=1-λ，n=λ．
∴m+n=1．
∵B，P，N三点共线，
∴存在实数λ使得
| BP |
| BN |
∴
| AP |
| AB |
| AN |
| AB |
∴
| AP |
| AN |
| AB |
又
| AP |
| AB |
| AN |
∴m=1-λ，n=λ．
∴m+n=1．
点评：本题考查了向量共线定理和平面向量基本定理，考查了推理能力和计算能力，属于中档题．
练习册系列答案
新思维小冠军100分作业本系列答案
名师指导一卷通系列答案
相关题目
已知抛物线C1：x2=2y的焦点为F，以F为圆心的圆C2交C1于A，B两点，交C1的准线于C，D两点，若四边形ABCD是矩形，则圆C2的方程为（ ）
| A、x2+（y-1）2=12 | ||
| B、x2+（y-1）2=16 | ||
C、x2+（y-
| ||
D、x2+（y-
|
下列函数中，既是奇函数，又在（0，+∞）上是减函数的是（ ）
A、y=
| ||
| B、y=x2 | ||
| C、y=x | ||
| D、y=-x+1 |
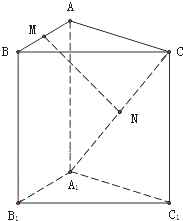在三棱柱ABC-A1B1C1中，M、N分别是AB、A1C的中点，求证：MN∥平面BCB1C1．