题目内容
已知抛物线C1:x2=2y的焦点为F,以F为圆心的圆C2交C1于A,B两点,交C1的准线于C,D两点,若四边形ABCD是矩形,则圆C2的方程为( )
| A、x2+(y-1)2=12 | ||
| B、x2+(y-1)2=16 | ||
C、x2+(y-
| ||
D、x2+(y-
|
考点:抛物线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:依题意知,圆C2的圆心坐标为F(0,
),且点F为该矩形ABCD的两条对角线的交点,利用点F到直线CD的距离与点F到AB的距离相等可求得直线AB的方程为:y=
,从而可求得A点坐标,从而可求得圆C2的半径,于是可得答案.
| 1 |
| 2 |
| 3 |
| 2 |
解答:
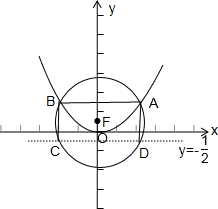 解:依题意,抛物线C1:x2=2y的焦点为F(0,
解:依题意,抛物线C1:x2=2y的焦点为F(0,
),
∴圆C2的圆心坐标为F(0,
),
∵四边形ABCD是矩形,且BD为直径,AC为直径,F(0,
)为圆C2的圆心,
∴点F为该矩形的两条对角线的交点,
∴点F到直线CD的距离与点F到AB的距离相等,
又点F到直线CD的距离d=1,
∴直线AB的方程为:y=
,
∴A(
,
),
∴圆C2的半径r=|AF|=
=2,
∴圆C2的方程为:x2+(y-
)2=4,
故选:D.
 解:依题意,抛物线C1:x2=2y的焦点为F(0,
解:依题意,抛物线C1:x2=2y的焦点为F(0,| 1 |
| 2 |
∴圆C2的圆心坐标为F(0,
| 1 |
| 2 |
∵四边形ABCD是矩形,且BD为直径,AC为直径,F(0,
| 1 |
| 2 |
∴点F为该矩形的两条对角线的交点,
∴点F到直线CD的距离与点F到AB的距离相等,
又点F到直线CD的距离d=1,
∴直线AB的方程为:y=
| 3 |
| 2 |
∴A(
| 3 |
| 3 |
| 2 |
∴圆C2的半径r=|AF|=
(
|
∴圆C2的方程为:x2+(y-
| 1 |
| 2 |
故选:D.
点评:本题考查抛物线的简单性质,考查圆的标准方程的确定,分析得到点F为该矩形ABCD的两条对角线的交点是关键,考查作图、分析与运算能力,属于中档题.

练习册系列答案
相关题目
若A、B、C三点共线,O是这条直线外一点,且满足m
-2
+
=
,若
=λ
,则λ的值为( )
| OA |
| OB |
| OC |
| 0 |
| BA |
| AC |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
设(2-x)5=a0+a1x+a2x2…+a5x5,那么
的值为( )
| a0+a2+a4 |
| a1+a3+a5 |
A、-
| ||
B、-
| ||
C、-
| ||
| D、-1 |
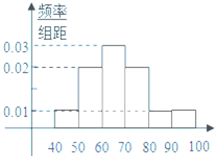 某高校从参加今年自主招生考试的1000名学生中随机抽取100名学生成绩进行统计,得到如图所示的样本频率分布直方图.若规定60分及以上为合格,则估计这1000名学生中合格人数是( )名.
某高校从参加今年自主招生考试的1000名学生中随机抽取100名学生成绩进行统计,得到如图所示的样本频率分布直方图.若规定60分及以上为合格,则估计这1000名学生中合格人数是( )名.| A、400 | B、600 |
| C、700 | D、800 |
“x>3”是“x2-5x+6>0”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分又不必要条件 |
空间有四个点,其中任意三点,都不在同一条直线上,那么它们可确定( )
| A、三个或两个平面 |
| B、四个或三个平面 |
| C、三个或一个平面 |
| D、四个或一个平面 |