题目内容
求函数f(x)=
+
的单调区间.
| x+2 |
| 4-x |
考点:利用导数研究函数的单调性,函数的单调性及单调区间
专题:计算题,导数的概念及应用
分析:确定函数的定义域,求导数,利用导数的正负可得函数的单调区间.
解答:
解:函数的定义域为[-2,4],
∵f(x)=
+
,
∴f′(x)=
-
=
,
令1-x>0,结合函数的定义域,可得函数的单调增区间为[-2,1);
令1-x<0,结合函数的定义域,可得函数的单调减区间为(1,4].
∵f(x)=
| x+2 |
| 4-x |
∴f′(x)=
| 1 | ||
2
|
| 1 | ||
2
|
| 1-x | ||||||||
2
|
令1-x>0,结合函数的定义域,可得函数的单调增区间为[-2,1);
令1-x<0,结合函数的定义域,可得函数的单调减区间为(1,4].
点评:本题主要考查通过求函数的导数确定函数增减区间的问题.当导数大于0时函数单调递增,当导数小于0时函数单调递减.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
“x>3”是“x2-5x+6>0”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分又不必要条件 |
 如图,在直三棱柱ABC-A1B1C1中,D、E分别为AA1、CC1的中点,AC⊥BE,点F在线段AB上,且AB=4AF,若M为线段BE上一点,试确定M在线段BE上的位置,使得C1D∥平面B1FM.
如图,在直三棱柱ABC-A1B1C1中,D、E分别为AA1、CC1的中点,AC⊥BE,点F在线段AB上,且AB=4AF,若M为线段BE上一点,试确定M在线段BE上的位置,使得C1D∥平面B1FM.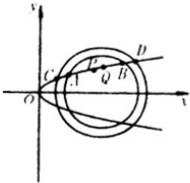 如图所示,设抛物线y2=2px,(0<p<1)与圆(x-5)2+y2=9在x轴上方的交点为A、B,与圆(x-6)2+y2=27在x轴上方的交点为C、D,P为AB中点,Q为CD的中点.
如图所示,设抛物线y2=2px,(0<p<1)与圆(x-5)2+y2=9在x轴上方的交点为A、B,与圆(x-6)2+y2=27在x轴上方的交点为C、D,P为AB中点,Q为CD的中点.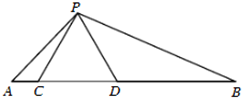 如图,点C、D在线段AB上,且△PCD是等边三角形.
如图,点C、D在线段AB上,且△PCD是等边三角形.