题目内容
等比数列{an}的各项均为正数,且a5a6+a3a8=6,则log3a1+log3a2+…+log3a10=( )
| A、6 |
| B、5 |
| C、4 |
| D、2+log35 |
考点:等比数列的性质
专题:计算题,等差数列与等比数列
分析:由题意可得a5a6=3,由等比数列的性质和对数的运算可得原式=log3(a5a6)5,化简可得.
解答:
解:由题意可得a5a6+a3a8=2a5a6=6,
解之可得a5a6=3,
故log3a1+log3a2+…+log3a10=log3(a1a2…a10)
=log3(a5a6)5=log335=5,
故选:B.
解之可得a5a6=3,
故log3a1+log3a2+…+log3a10=log3(a1a2…a10)
=log3(a5a6)5=log335=5,
故选:B.
点评:本题考查等比数列的通项公式和性质,涉及对数的运算性质,属基础题.

练习册系列答案
相关题目
已知命题p:存在x∈R,使得x-10>lgx;命题q:对任意x∈R,都有x2>0,则( )
| A、命题“p或q”是假命题 |
| B、命题“p且q”是真命题 |
| C、命题“非q”是假命题 |
| D、命题“p且‘非q’”是真命题 |
在等比数列{an}中,a1=27,a4=a3a5,则a6=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
设f(x)是定义在R上的偶函数,?x∈R,都有f(2-x)=f(2+x),且当x∈[0,2]时,f(x)=2x-2,若函数g(x)=f(x)-loga(x+1)(a>0,a≠1)在区间(-1,9]内恰有三个不同零点,则实数a的取值范围是( )
A、(0,
| ||||||||
B、(
| ||||||||
C、(
| ||||||||
D、(
|
设函数f(x)=|sin(2x+
)|,则下列关于函数f(x)的说法中正确的是( )
| π |
| 3 |
A、f(x)图象关于直线x=
| ||||
| B、f(x)的最小正周期为π | ||||
C、f(x)图象关于点(-
| ||||
D、f(x)在区间[
|
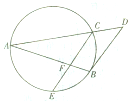 如图,已知AB、AC、CE是圆的弦,过点B作圆的切线与AC的延长线相交于点D,且
如图,已知AB、AC、CE是圆的弦,过点B作圆的切线与AC的延长线相交于点D,且