题目内容
设f(x)是定义在R上的偶函数,?x∈R,都有f(2-x)=f(2+x),且当x∈[0,2]时,f(x)=2x-2,若函数g(x)=f(x)-loga(x+1)(a>0,a≠1)在区间(-1,9]内恰有三个不同零点,则实数a的取值范围是( )
A、(0,
| ||||||||
B、(
| ||||||||
C、(
| ||||||||
D、(
|
考点:函数奇偶性的性质
专题:
分析:由f(x)是定义在R上的偶函数,且f(2+x)=f(2-x),推出函数f(x)是以4为最小正周期的函数,结合题意画出在区间(-1,9)内函数f(x)和y=loga(x+1)的图象,注意对a讨论,分a>1,0<a<1,结合图象即可得到a的取值范围.
解答:
解:∵f(x)是定义在R上的偶函数,
∴f(2+x)=f(2-x)=f(x-2),
即f(x+4)=f(x)
∴f(x+4)=f(x),
则函数f(x)是以4为最小正周期的函数,
∵当x∈[0,2]时,f(x)=2x-2,
f(x)是定义在R上的偶函数,
∴当x∈[-2,0]时,f(x)=f(-x)=2-x-1,
结合题意画出函数f(x)在x∈(-1,9]上的图象
与函数y=loga(x+1)的图象,
①若0<a<1,要使f(x)与y=loga(x+1)的图象,恰有3个交点,
则
,
即
,
解得
即a∈(
,
),
②若a>1,要使f(x)与y=loga(x+1)的图象,恰有3个交点,
则
,
即
解得
,
即a∈(
,
),
综上a的取值范围是(
,
)∪(
,
)
故选:C.
∴f(2+x)=f(2-x)=f(x-2),
即f(x+4)=f(x)

∴f(x+4)=f(x),
则函数f(x)是以4为最小正周期的函数,
∵当x∈[0,2]时,f(x)=2x-2,
f(x)是定义在R上的偶函数,
∴当x∈[-2,0]时,f(x)=f(-x)=2-x-1,
结合题意画出函数f(x)在x∈(-1,9]上的图象
与函数y=loga(x+1)的图象,
①若0<a<1,要使f(x)与y=loga(x+1)的图象,恰有3个交点,
则
|
即
|
解得
|
即a∈(
| 1 |
| 9 |
| 1 |
| 5 |
②若a>1,要使f(x)与y=loga(x+1)的图象,恰有3个交点,
则
|
即
|
解得
|

即a∈(
| 3 |
| 7 |
综上a的取值范围是(
| 1 |
| 9 |
| 1 |
| 5 |
| 3 |
| 7 |
故选:C.
点评:本题主要考查函数的奇偶性和周期性及其运用,同时考查数形结合的数学思想方法,以及对底数a的讨论.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
等比数列{an}的各项均为正数,且a5a6+a3a8=6,则log3a1+log3a2+…+log3a10=( )
| A、6 |
| B、5 |
| C、4 |
| D、2+log35 |
已知f(x)=|x-1|+|x+m|(m∈R),g(x)=2x-1,若m>-1,x∈[-m,1],不等式f(x)<g(x)恒成立,则实数m的取值范围是( )
A、(-1,-
| ||
B、(-1,-
| ||
C、(-∞,-
| ||
| D、(-1,+∞) |
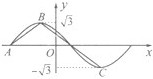 如图为函数f(x)=
如图为函数f(x)=| 3 |
| AB |
| BC |
| AB |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知i为虚数单位,则
的共轭复数的实部与虚部的乘积等于( )
| i |
| 1+i |
A、-
| ||
B、
| ||
C、
| ||
D、-
|
数列{an}的前n项和sn,若a1=1,an=
,Sn=124,则n=( )
|
| A、8 | B、9 | C、10 | D、11 |
已知复数z=
(i为虚数单位),则z的共轭复数为( )
| i | ||
|
A、
| ||||||
B、
| ||||||
C、-1-
| ||||||
D、-1+
|
某工厂安排甲、乙两种产品的生产,已知工厂生产每吨甲、乙两种产品所需要的原材料A、B、C的数量和一周内可用资源数量如下表所示:
如果甲产品每吨的利润为300元,乙产品每吨的利润为200元,此处不考虑市场的有限性,则工厂每周要获得最大利润,最科学的安排生产方式是( )
| 原材料 | 甲(吨) | 乙(吨) | 资源数量(吨) |
| A | 1 | 1 | 50 |
| B | 4 | 0 | 160 |
| C | 2 | 5 | 200 |
| A、每周生产甲产品40吨,不生产乙产品 | ||||
| B、每周不生产甲产品,生产乙产品40吨 | ||||
C、每周生产甲产品
| ||||
| D、每周生产甲产品40吨,生产乙产品10吨 |