Question

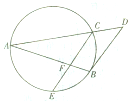如图，已知AB、AC、CE是圆的弦，过点B作圆的切线与AC的延长线相交于点D，且

AC

CD

=

AF

FB

，AF=3，FB=1，EF=

3

2

，则线段CD的长为

 

．

Answer 1

考点：与圆有关的比例线段,弦切角

专题：选作题,立体几何

分析：由相交弦定理求出FC，由相似比求出BD，设DC=x，则AD=4x，再由切割线定理，BD²=CD•AD求解．

解答： 解：由相交弦定理得到AF•FB=EF•FC，即3×1=

3

2

×FC，FC=2，
在△ABD中，

AC

CD

=

AF

FB

，
∴CF∥BD，
∴AF：AB=FC：BD，即3：4=2：BD，
∴BD=

8

3

，
设DC=x，则AD=4x，再由切割线定理，BD²=CD•AD，即x•4x=（

8

3

）²，
∴x=

4

3

．
故答案为：

4

3

．

点评：本题考查相交弦定理，考查切割线定理，考查学生的计算能力，属于基础题．