题目内容
8.已知双曲线${C_1}:\frac{x^2}{4}-{y^2}=1$,双曲线${C_2}:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>b>0)$的左、右焦点分别为F1,F2,M是双曲线C2的一条渐近线上的点,且OM⊥MF2,O为坐标原点,若${S_{△OM{F_2}}}=16$,且双曲线C1,C2的离心率相同,则双曲线C2的实轴长是( )| A. | 32 | B. | 16 | C. | 8 | D. | 4 |
分析 求得双曲线C1的离心率,求得双曲线C2一条渐近线方程为y=$\frac{b}{a}$x,运用点到直线的距离公式,结合勾股定理和三角形的面积公式,化简整理解方程可得a=8,进而得到双曲线的实轴长.
解答 解:双曲线${C_1}:\frac{x^2}{4}-{y^2}=1$的离心率为$\frac{\sqrt{5}}{2}$,
设F2(c,0),双曲线C2一条渐近线方程为y=$\frac{b}{a}$x,
可得|F2M|=$\frac{bc}{\sqrt{{a}^{2}+{b}^{2}}}$=b,
即有|OM|=$\sqrt{{c}^{2}-{b}^{2}}$=a,
由${S_{△OM{F_2}}}=16$,可得$\frac{1}{2}$ab=16,
即ab=32,又a2+b2=c2,且$\frac{c}{a}$=$\frac{\sqrt{5}}{2}$,
解得a=8,b=4,c=4$\sqrt{5}$,
即有双曲线的实轴长为16.
故选:B.
点评 本题考查双曲线的方程和性质,注意运用点到直线的距离公式和离心率公式,考查化简整理的运算能力,属于中档题.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案
相关题目
19.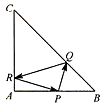 在等腰直角三角形ABC中,AB=AC=4,点P是边AB上异于A,B的一点,光线从点P出发,经BC,CA发射后又回到原点P(如图11).若光线QR经过△ABC的重心,则BP等于( )
在等腰直角三角形ABC中,AB=AC=4,点P是边AB上异于A,B的一点,光线从点P出发,经BC,CA发射后又回到原点P(如图11).若光线QR经过△ABC的重心,则BP等于( )
 在等腰直角三角形ABC中,AB=AC=4,点P是边AB上异于A,B的一点,光线从点P出发,经BC,CA发射后又回到原点P(如图11).若光线QR经过△ABC的重心,则BP等于( )
在等腰直角三角形ABC中,AB=AC=4,点P是边AB上异于A,B的一点,光线从点P出发,经BC,CA发射后又回到原点P(如图11).若光线QR经过△ABC的重心,则BP等于( )| A. | 2 | B. | 1 | C. | $\frac{8}{3}$ | D. | $\frac{4}{3}$ |
3.在矩形ABCD中,AB=2,AD=1,点P为矩形ABCD内一点,则使得$\overrightarrow{AP}$•$\overrightarrow{AC}$≥1的概率为$\frac{7}{8}$.
20.下列说法中正确的是( )
| A. | 经过不同的三点有且只有一个平面 | |
| B. | 没有公共点的两条直线一定平行 | |
| C. | 垂直于同一平面的两直线是平行直线 | |
| D. | 垂直于同一平面的两平面是平行平面 |