题目内容
3.在矩形ABCD中,AB=2,AD=1,点P为矩形ABCD内一点,则使得$\overrightarrow{AP}$•$\overrightarrow{AC}$≥1的概率为$\frac{7}{8}$.分析 将矩形放在坐标系中,设P(x,y)利用向量的数量积公式,作出对应的区域,求出对应的面积即可得到结论.
解答 解:将矩形放在坐标系中,设P(x,y),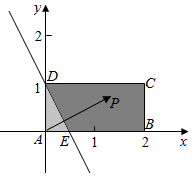
则A(0,0),C(2,1),
则$\overrightarrow{AP}$•$\overrightarrow{AC}$≥1等价为2x+y≥1,
作出不等式对应的区域,为五边形DCBE,
当y=0时,x=$\frac{1}{2}$,即E($\frac{1}{2}$,0),
则△ADE的面积S=$\frac{1}{2}$×$\frac{1}{2}$×$1=\frac{1}{4}$,
则五边形DCBE的面积S=2-$\frac{1}{4}$=$\frac{7}{4}$,
则$\overrightarrow{AP}$•$\overrightarrow{AC}$≥1的概率P=$\frac{7}{8}$,
故答案为$\frac{7}{8}$.
点评 本题主要考查几何概型的概率的计算,根据向量数量积的坐标关系,求出对应区域面积,是解决本题的关键.

练习册系列答案
相关题目
14.已知菱形ABCD的边长为4,∠ABC=120°,若在菱形内任取一点,则该点到菱形的四个顶点的距离大于1的概率( )
| A. | $\frac{π}{4}$ | B. | 1-$\frac{π}{4}$ | C. | $\frac{{\sqrt{3}π}}{24}$ | D. | $1-\frac{{\sqrt{3}π}}{24}$ |
11.不存在函数f(x)满足,对任意x∈R都有( )
| A. | f(|x+1|)=x2+2x | B. | f(cos2x)=cosx | C. | f(sinx)=cos2x | D. | f(cosx)=cos2x |
12.已知函数f(x)=$\frac{1}{2}$x2+2xf′(2017)-2017lnx,则f′(2017)=( )
| A. | 2016 | B. | -2016 | C. | 2017 | D. | -2017 |
13.取一根长度为4m的绳子,拉直后在任意位置剪断,则剪得的两段长度都不小于1.5m的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |