题目内容
20．下列说法中正确的是（ ）| A． | 经过不同的三点有且只有一个平面 | |
| B． | 没有公共点的两条直线一定平行 | |
| C． | 垂直于同一平面的两直线是平行直线 | |
| D． | 垂直于同一平面的两平面是平行平面 |
分析 反例判断A的正误；异面直线判断B的正误；直线与平面垂直的性质判断C的正误；反例判断D的正误；
解答 解：如果三个点在一条直线上，则经过不同的三点有无数个平面，所以A不正确；
由异面直线的定义，可知没有公共点的两条直线可能是平行，也可能异面．所以B不正确；
由直线与平面垂直的性质可知：垂直于同一平面的两直线是平行直线，正确；
垂直于同一平面的两平面是平行平面，可能是相交平面，所以D 不正确；
故选：C．
点评 本题考查空间直线与平面，直线与直线，平面与平面的位置关系的判断，熟练掌握基本定理与性质的解题的关键．
练习册系列答案
口算题天天练系列答案
相关题目
10．下列说法正确的是（ ）
| A． | 命题“若x2=1，则x=1的否命题为：“若x2=1，则x≠1” | |
| B． | “m=1”是“直线x-my=0和直线x+my=0互相垂直”的充要条件 | |
| C． | 命题“?x0∈R，使得x02+x0+1＜0”的否定是：“?x∈R，均有x2+x+1＜0” | |
| D． | 命题“已知A，B为一个三角形两内角，若A=B，则sinA=sinB”的否命题为真命题 |
11．不存在函数f（x）满足，对任意x∈R都有（ ）
| A． | f（|x+1|）=x2+2x | B． | f（cos2x）=cosx | C． | f（sinx）=cos2x | D． | f（cosx）=cos2x |
5．已知抛物线y2=2px的准线方程是x=-2，则p的值为（ ）
| A． | 2 | B． | 4 | C． | -2 | D． | -4 |
12．已知函数f（x）=$\frac{1}{2}$x2+2xf′（2017）-2017lnx，则f′（2017）=（ ）
| A． | 2016 | B． | -2016 | C． | 2017 | D． | -2017 |
9．
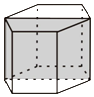如图，已知正六棱柱的最大对角面的面积为4m2，互相平行的两个侧面的距离为 2m，则这个六棱柱的体积为（ ）
如图，已知正六棱柱的最大对角面的面积为4m2，互相平行的两个侧面的距离为 2m，则这个六棱柱的体积为（ ）| A． | 3m3 | B． | 6m3 | C． | 12m3 | D． | 15m3 |
10．集合M={x|lg（1-x）＜1}，N={x|-1≤x≤1}，则M∩N=（ ）
| A． | （-9，1） | B． | （-9，1] | C． | [-1，1] | D． | [-1，1） |