题目内容
15.已知$α∈({0,\frac{π}{2}})$,且$2cos2α=cos({\frac{π}{4}-α})$,则sin2α的值为( )| A. | $\frac{1}{8}$ | B. | $-\frac{1}{8}$ | C. | $\frac{7}{8}$ | D. | $-\frac{7}{8}$ |
分析 由条件利用两角和的正弦公式、二倍角公式求得cosα-sinα,或 cosα+sinα的值,由此求得sin2α的值.
解答 解:∵$α∈({0,\frac{π}{2}})$,且$2cos2α=cos({\frac{π}{4}-α})$,
∴2(cos2α-sin2α)=$\frac{\sqrt{2}}{2}$(cosα+sinα),
∴cosα-sinα=$\frac{\sqrt{2}}{4}$,或 cosα+sinα=0.
当cosα-sinα=$\frac{\sqrt{2}}{4}$,则有1-sin2α=$\frac{1}{8}$,sin2α=$\frac{7}{8}$;
∵α∈(0,$\frac{π}{2}$),
∴cosα+sinα=0不成立,
故选:C.
点评 本题主要考查两角和差的正弦、余弦公式的应用,二倍角公式的应用,考查了转化思想,属于基础题.

练习册系列答案
相关题目
5.函数y=2xex的一个原函数为( )
| A. | 2xex(1+ln2) | B. | $\frac{{2}^{x}{e}^{x}}{(1+ln2)}$ | C. | 2exln2 | D. | $\frac{2{e}^{x}}{ln2}$ |
10.椭圆$C:\frac{x^2}{4}+\frac{y^2}{3}=1$与双曲线$E:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a,b>0)$有相同的焦点,且两曲线的离心率互为倒数,则双曲线渐近线的倾斜角的正弦值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
7.在△ABC所在平面上有一点P,满足$\overrightarrow{PA}+\overrightarrow{PB}+\overrightarrow{PC}=\overrightarrow{BC}$,$\overrightarrow{PC}=x\overrightarrow{AB}+y\overrightarrow{AC}$,则x+y=( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $-\frac{1}{3}$ | D. | $-\frac{1}{2}$ |
5.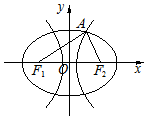 如图,椭圆与双曲线有公共焦点F1,F2,它们在第一象限的交点为A,且AF1⊥AF2
如图,椭圆与双曲线有公共焦点F1,F2,它们在第一象限的交点为A,且AF1⊥AF2
∠AF1F2=30°,则椭圆与双曲线的离心率的之积为( )
 如图,椭圆与双曲线有公共焦点F1,F2,它们在第一象限的交点为A,且AF1⊥AF2
如图,椭圆与双曲线有公共焦点F1,F2,它们在第一象限的交点为A,且AF1⊥AF2∠AF1F2=30°,则椭圆与双曲线的离心率的之积为( )
| A. | 2 | B. | $\sqrt{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
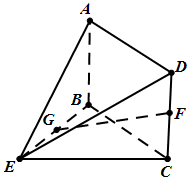 如图,在几何体ABCDE中,四边形ABCD是矩形,AB⊥平面BCE,BE⊥CE,AB=BE=EC=2,G,F分别是线段BE,DC的中点.
如图,在几何体ABCDE中,四边形ABCD是矩形,AB⊥平面BCE,BE⊥CE,AB=BE=EC=2,G,F分别是线段BE,DC的中点.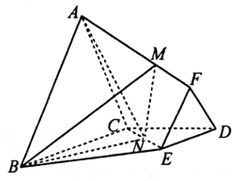 如图,在棱台ABC-FED中,△DEF与△ABC分别是棱长为1与2的正三角形,平面ABC⊥平面BCDE,四边形BCDE为直角梯形,BC⊥CD,CD=1,N为CE中点,$\overrightarrow{AM}=λ\overrightarrow{AF}({λ∈R,λ>0})$.
如图,在棱台ABC-FED中,△DEF与△ABC分别是棱长为1与2的正三角形,平面ABC⊥平面BCDE,四边形BCDE为直角梯形,BC⊥CD,CD=1,N为CE中点,$\overrightarrow{AM}=λ\overrightarrow{AF}({λ∈R,λ>0})$. 18、甲、乙两位同学参加数学文化知识竞赛培训,现分别从他们在培训期间参加的若干次测试成绩中随机抽取8次,记录如下:
18、甲、乙两位同学参加数学文化知识竞赛培训,现分别从他们在培训期间参加的若干次测试成绩中随机抽取8次,记录如下: