题目内容
6.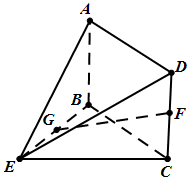 如图,在几何体ABCDE中,四边形ABCD是矩形,AB⊥平面BCE,BE⊥CE,AB=BE=EC=2,G,F分别是线段BE,DC的中点.
如图,在几何体ABCDE中,四边形ABCD是矩形,AB⊥平面BCE,BE⊥CE,AB=BE=EC=2,G,F分别是线段BE,DC的中点.(I)求证:GF∥平面ADE;
(II)求GF与平面ABE所成角的正切值.
分析 (Ⅰ)取AE的中点H,连接HG,HD,由G是BE的中点,F是CD中点,推导出四边形HGFD是平行四边形,从而GF∥DH,由此能证明GF∥平面ADE.
(II)过B作BQ∥EC,以D为原点,BE、BQ、BA所在直线分别为x,y,z轴,建立空间直角坐标系,利用向量法能求出GF与平面ABE所成角的正切值.
解答 证明:(Ⅰ)如图,取AE的中点H,连接HG,HD,又G是BE的中点,
∴GH∥AB,且GH=$\frac{1}{2}$AB,
又F是CD中点,∴DF=$\frac{1}{2}$CD,
由四边形ABCD是矩形得,AB∥CD,AB=CD,
∴GH∥DF,且GH=DF.∴四边形HGFD是平行四边形,
∴GF∥DH,又DH?平面ADE,GF?平面ADE,
∴GF∥平面ADE.
解:(II)如图,在平面BEC内,过B作BQ∥EC,
∵BE⊥CE,∴BQ⊥BE,
又∵AB⊥平面BEC,∴AB⊥BE,AB⊥BQ,
以D为原点,BE、BQ、BA所在直线分别为x,y,z轴,建立空间直角坐标系,
则A(0,0,2),B(0,0,0),E(2,0,0),F(2,2,1),G(1,0,0),
$\overrightarrow{GF}$=(1,2,1),平面ABE的法向量$\overrightarrow{n}$=(0,1,0),
设GF与平面ABE所成角的平面角为θ,
则sinθ=$\frac{|\overrightarrow{GF}•\overrightarrow{n}|}{|\overrightarrow{GF}|•|\overrightarrow{n}|}$=$\frac{2}{\sqrt{6}}$,∴cosθ=$\sqrt{1-(\frac{2}{\sqrt{6}})^{2}}$=$\frac{\sqrt{2}}{\sqrt{6}}$,
∴tanθ=$\frac{sinθ}{cosθ}$=$\frac{\frac{2}{\sqrt{6}}}{\frac{\sqrt{2}}{\sqrt{6}}}$=$\sqrt{2}$.
∴GF与平面ABE所成角的正切值为$\sqrt{2}$.
点评 本题考查线面平行的证明,考查线面角的正切值的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查空间想象能力、推理论证能力、运算求解能力,考查数形结合思想、化归与转化思想,是中档题.

| A. | {x|-1<x≤$\frac{1}{3}$} | B. | {x|x≥$\frac{1}{3}$} | C. | {x|x≤$\frac{1}{3}$} | D. | {x|$\frac{1}{3}$≤x<1} |
| A. | 32 | B. | 64 | C. | 128 | D. | 256 |
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{4}{5}$ | D. | 1 |
| A. | $[{\frac{π}{12},\frac{π}{4}}]$ | B. | $[{\frac{π}{6},\frac{5π}{12}})$ | C. | $[{\frac{π}{6},\frac{π}{3}}]$ | D. | $({\frac{π}{6},\frac{π}{4}}]$ |
| A. | 2-i | B. | 2+i | C. | 4-i | D. | 4+i |
| A. | $\frac{1}{8}$ | B. | $-\frac{1}{8}$ | C. | $\frac{7}{8}$ | D. | $-\frac{7}{8}$ |
| 同意限定区域停车 | 不同意限定区域停车 | 合计 | |
| 男 | 18 | 7 | 25 |
| 女 | 12 | 13 | 25 |
| 合计 | 30 | 20 | 50 |
(Ⅱ)已知在同意限定区域停车的12位女性家长中,有3位日常开车接送孩子.现从这12位女性家长中随机抽取3人参与维持秩序,记参与维持秩序的女性家长中,日常开车接送孩子的女性家长人数为ξ,求ξ的分布列和数学期望.
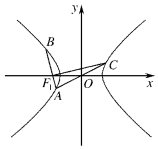 如图,过双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)左焦点F1的直线交双曲线左支于A,B两点,C是双曲线右支上一点,且A,C在x轴的异侧,若满足|OA|=|OF1|=|OC|,|CF1|=2|BF1|,则双曲线的离心率为$\frac{\sqrt{17}}{3}$.
如图,过双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)左焦点F1的直线交双曲线左支于A,B两点,C是双曲线右支上一点,且A,C在x轴的异侧,若满足|OA|=|OF1|=|OC|,|CF1|=2|BF1|,则双曲线的离心率为$\frac{\sqrt{17}}{3}$.