题目内容
20.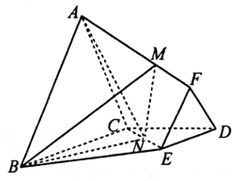 如图,在棱台ABC-FED中,△DEF与△ABC分别是棱长为1与2的正三角形,平面ABC⊥平面BCDE,四边形BCDE为直角梯形,BC⊥CD,CD=1,N为CE中点,$\overrightarrow{AM}=λ\overrightarrow{AF}({λ∈R,λ>0})$.
如图,在棱台ABC-FED中,△DEF与△ABC分别是棱长为1与2的正三角形,平面ABC⊥平面BCDE,四边形BCDE为直角梯形,BC⊥CD,CD=1,N为CE中点,$\overrightarrow{AM}=λ\overrightarrow{AF}({λ∈R,λ>0})$.(Ⅰ)λ为何值时,MN∥平面ABC?
(Ⅱ)在(Ⅰ)的条件下,求直线AN与平面BMN所成角的正弦值.
分析 (Ⅰ)取CD中点P,连接PM,PN,可得MP∥AC,则MP∥平面ABC.再由已知证明NP∥平面ABC.得到平面MNP∥平面ABC,则MN∥平面ABC;
(Ⅱ)取BC中点O,连OA,OE,可证AO⊥BC,OE⊥BC.分别以OE,OC,OA所在直线为x轴,y轴,z轴,建立空间直角坐标系.求出所用点的坐标,得到平面BMN的法向量,求出<$\overrightarrow{AN},\overrightarrow{n}$>的余弦值,即可得到直线AN与平面MNB所成角的正弦值.
解答 解:(Ⅰ)当$λ=\frac{1}{2}$,即M为AF中点时MN∥平面ABC.
事实上,取CD中点P,连接PM,PN,
∵AM=MF,CP=PD,∴MP∥AC,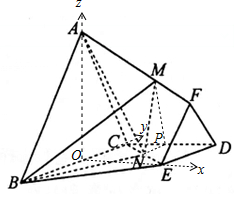
∵AC?平面ABC,MP?平面ABC,∴MP∥平面ABC.
由CP∥PD,CN∥NE,得NP∥DE,
又DE∥BC,∴NP∥BC,
∵BC?平面ABC,NP?平面ABC,∴NP∥平面ABC.
∴平面MNP∥平面ABC,则MN∥平面ABC;
(Ⅱ)取BC中点O,连OA,OE,
∵AB=AC,OB=OC,∴AO⊥BC,
∵平面ABC⊥平面BCDE,且AO?平面ABC,∴AO⊥平面BCDE,
∵OC=$\frac{1}{2}BC=ED$,BC∥ED,∴OE∥CD,
又CD⊥BC,∴OE⊥BC.
分别以OE,OC,OA所在直线为x轴,y轴,z轴,建立空间直角坐标系.
则A(0,0,$\sqrt{3}$),C(0,1,0),E(1,0,0),$\overrightarrow{EF}=\frac{1}{2}\overrightarrow{BA}=(0,\frac{1}{2},\frac{\sqrt{3}}{2})$,
∴F(1,$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),M($\frac{1}{2}$,$\frac{1}{4}$,$\frac{3\sqrt{3}}{4}$),N($\frac{1}{2},\frac{1}{2},0$).
设$\overrightarrow{n}=(x,y,z)$为平面BMN的法向量,则
$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{BN}=\frac{x}{2}+\frac{3}{2}y=0}\\{\overrightarrow{n}•\overrightarrow{MN}=-\frac{y}{4}+\frac{3\sqrt{3}}{4}z=0}\end{array}\right.$,取z=1,得$\overrightarrow{n}=(-9\sqrt{3},3\sqrt{3},1)$.
cos<$\overrightarrow{AN},\overrightarrow{n}$>=$\frac{-4\sqrt{6}}{\sqrt{1897}}$.
∴直线AN与平面MNB所成角的正弦值为$\frac{4\sqrt{6}}{\sqrt{1897}}$.
点评 本题考查直线与平面平行的判定,考查空间想象能力和思维能力,训练了利用空间向量求线面角,是中档题.

 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案| A. | (-∞,0)∪(0,$\frac{1}{2}$) | B. | (-∞,$\frac{1}{2}$) | C. | ($\frac{1}{2}$,+∞) | D. | (0,$\frac{1}{2}$) |
| A. | $[{\frac{π}{12},\frac{π}{4}}]$ | B. | $[{\frac{π}{6},\frac{5π}{12}})$ | C. | $[{\frac{π}{6},\frac{π}{3}}]$ | D. | $({\frac{π}{6},\frac{π}{4}}]$ |
| A. | $\frac{1}{8}$ | B. | $-\frac{1}{8}$ | C. | $\frac{7}{8}$ | D. | $-\frac{7}{8}$ |
| A. | ?x0>2,${2^{x_0}}-3≤0$ | B. | ?x≤2,2x-3>0 | C. | ?x>2,2x-3≤0 | D. | ?x0>2,${2^{x_0}}-3>0$ |
| A. | [0,+∞) | B. | (1,+∞) | C. | [0,1) | D. | (0,+∞) |
| A. | ?x≤0,lnx0>x0 | B. | ?x≤0,lnx0≥x0 | C. | ?x>0,lnx0≥x0 | D. | ?x>0,lnx0<x0 |
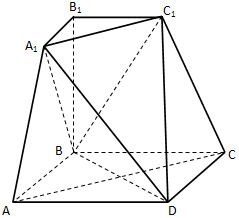 如图所示的几何体是由棱台ABC-A1B1C1和棱锥D-AA1C1C拼接而成的组合体,其底面四边形ABCD是边长为2的菱形,且∠BAD=60°,BB1⊥平面ABCD,BB1=2A1B1=2.
如图所示的几何体是由棱台ABC-A1B1C1和棱锥D-AA1C1C拼接而成的组合体,其底面四边形ABCD是边长为2的菱形,且∠BAD=60°,BB1⊥平面ABCD,BB1=2A1B1=2.