题目内容
5．
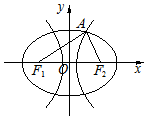如图，椭圆与双曲线有公共焦点F1，F2，它们在第一象限的交点为A，且AF1⊥AF2∠AF1F2=30°，则椭圆与双曲线的离心率的之积为（ ）
| A． | 2 | B． | $\sqrt{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{\sqrt{3}}{2}$ |
分析 运用椭圆和双曲线的定义，结合离心率公式和解直角三角形的有关知识，化简计算即可得到．
解答 
解：设椭圆的长轴长为2a1，焦距为2c，双曲线的实轴长2a2，焦距为2c，
由椭圆的定义可知，丨AF1丨+丨AF2丨=2a1，
由双曲线的定义：丨AF1丨-丨AF2丨=2a2，
在Rt△AF1F2中，∠AF1F2=30°，
则丨AF2丨=$\frac{1}{2}$丨F1F2丨=c，丨AF1丨=$\frac{\sqrt{3}}{2}$丨F1F2丨=$\sqrt{3}$c，
则有2a1=（$\sqrt{3}$+1）c，2a2=（$\sqrt{3}$-1）c，
则离心率e1=$\frac{c}{{a}_{1}}$=$\frac{2}{\sqrt{3}+1}$，e2=$\frac{c}{{a}_{2}}$=$\frac{2}{\sqrt{3}-1}$，
e1×e2=$\frac{2}{\sqrt{3}+1}$×$\frac{2}{\sqrt{3}-1}$=2，
则椭圆与双曲线的离心率的之积2，
故选：A．
点评 本题考查椭圆和双曲线的定义和性质，考查离心率公式，三角形的性质，考查运算能力，属于中档题．
练习册系列答案
相关题目
15．已知$α∈（{0，\frac{π}{2}}）$，且$2cos2α=cos（{\frac{π}{4}-α}）$，则sin2α的值为（ ）
| A． | $\frac{1}{8}$ | B． | $-\frac{1}{8}$ | C． | $\frac{7}{8}$ | D． | $-\frac{7}{8}$ |
16．某学校为了制定治理学校门口上学、方向期间家长接送孩子乱停车现象的措施，对全校学生家长进行了问卷调查．根据从其中随机抽取的50份调查问卷，得到了如下的列联表．
（Ⅰ）学校计划在同意限定区域停车的家长中，按照分层抽样的方法，随机抽取5人在上学、放学期间在学校门口参与维持秩序．在随机抽取的5人中，选出2人担任召集人，求至少有一名女性的概率？
（Ⅱ）已知在同意限定区域停车的12位女性家长中，有3位日常开车接送孩子．现从这12位女性家长中随机抽取3人参与维持秩序，记参与维持秩序的女性家长中，日常开车接送孩子的女性家长人数为ξ，求ξ的分布列和数学期望．
| 同意限定区域停车 | 不同意限定区域停车 | 合计 | |
| 男 | 18 | 7 | 25 |
| 女 | 12 | 13 | 25 |
| 合计 | 30 | 20 | 50 |
（Ⅱ）已知在同意限定区域停车的12位女性家长中，有3位日常开车接送孩子．现从这12位女性家长中随机抽取3人参与维持秩序，记参与维持秩序的女性家长中，日常开车接送孩子的女性家长人数为ξ，求ξ的分布列和数学期望．
13．“a＞0”是“$a+\frac{2}{a}≥2\sqrt{2}$”的（ ）
| A． | 充分而不必要条件 | B． | 必要而不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
20．2014年5月12日，国家统计局公布了《2013年农民工监测调查报告》，报告显示：我国农民工收入持续快速增长．某地区农民工人均月收入增长率如图1，并将人均月收入绘制成如图2的不完整的条形统计图．
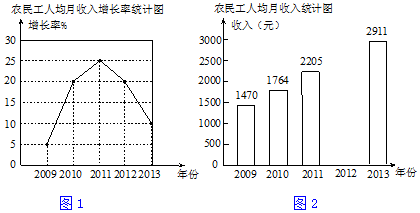
根据以上统计图来判断以下说法错误的是（ ）
根据以上统计图来判断以下说法错误的是（ ）
| A． | 2013年农民工人均月收入的增长率是10% | |
| B． | 2011年农民工人均月收入是2205元 | |
| C． | 小明看了统计图后说：“农民工2012年的人均月收入比2011年的少了” | |
| D． | 2009年到2013年这五年中2013年农民工人均月收入最高 |
17．已知$sin（α-\frac{π}{12}）=\frac{1}{3}$，则$cos（α+\frac{5π}{12}）$的值等于（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{{2\sqrt{2}}}{3}$ | C． | $-\frac{1}{3}$ | D． | $-\frac{{2\sqrt{2}}}{3}$ |