题目内容
11.设函数$f(x)=\frac{2}{3}+\frac{1}{x}({x>0})$,数列{an}满足${a_1}=1,{a_n}=f({\frac{1}{{{a_{n-1}}}}})$,n∈N*,且n≥2.(1)求数列{an}的通项公式;
(2)对n∈N*,设${S_n}=\frac{1}{{{a_1}{a_2}}}+\frac{1}{{{a_2}{a_3}}}+\frac{1}{{{a_3}{a_4}}}+…+\frac{1}{{{a_n}{a_{n+1}}}}$,若${S_n}≥\frac{3t}{4n}$恒成立,求实数t的取值范围.
分析 (1)通过代入计算可知an-an-1=$\frac{2}{3}$(n≥2),进而可知数列{an}是首项为1、公差为$\frac{2}{3}$的等差数列,计算即得结论;
(2)通过(1)裂项可知$\frac{1}{{a}_{n}{a}_{n+1}}$=$\frac{9}{2}$($\frac{1}{2n+1}$-$\frac{1}{2n+3}$),进而并项相加可知Sn=$\frac{3n}{2n+3}$,问题转化为求$\frac{4{n}^{2}}{2n+3}$的最小值,通过令g(x)=$\frac{4{x}^{2}}{2x+3}$(x>0),求导可知g(x)为增函数,进而计算可得结论.
解答 解:(1)依题意,an-an-1=$\frac{2}{3}$(n≥2),
又∵a1=1,
∴数列{an}是首项为1、公差为$\frac{2}{3}$的等差数列,
故其通项公式an=1+$\frac{2}{3}$(n-1)=$\frac{2n+1}{3}$;
(2)由(1)可知an+1=$\frac{2n+3}{3}$,
∴$\frac{1}{{a}_{n}{a}_{n+1}}$=$\frac{9}{2}$($\frac{1}{2n+1}$-$\frac{1}{2n+3}$),
∴${S_n}=\frac{1}{{{a_1}{a_2}}}+\frac{1}{{{a_2}{a_3}}}+\frac{1}{{{a_3}{a_4}}}+…+\frac{1}{{{a_n}{a_{n+1}}}}$
=$\frac{9}{2}$($\frac{1}{3}$-$\frac{1}{5}$+$\frac{1}{5}$-$\frac{1}{7}$+…+$\frac{1}{2n+1}$-$\frac{1}{2n+3}$)
=$\frac{3n}{2n+3}$,
${S_n}≥\frac{3t}{4n}$恒成立等价于$\frac{3n}{2n+3}$≥$\frac{3t}{4n}$,即t≤$\frac{4{n}^{2}}{2n+3}$恒成立.
令g(x)=$\frac{4{x}^{2}}{2x+3}$(x>0),则g′(x)=$\frac{8x(x+3)}{(2x+3)^{2}}$>0,
∴g(x)=$\frac{4{x}^{2}}{2x+3}$(x>0)为增函数,
∴当n=1时$\frac{4{n}^{2}}{2n+3}$取最小值$\frac{4}{5}$,
故实数t的取值范围是(-∞,$\frac{4}{5}$].
点评 本题考查数列的通项及前n项和,考查裂项相消法,考查利用导数判断函数的单调性,注意解题方法的积累,属于中档题.

 金博士一点全通系列答案
金博士一点全通系列答案| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | $\sqrt{5}$ | B. | $\sqrt{2}$ | C. | 2 | D. | $\frac{{\sqrt{5}}}{2}$ |
①若x1y2-x2y1=0,则$\overrightarrow a∥\overrightarrow b$;
②若x1x2+y1y2=0,则$\overrightarrow a⊥\overrightarrow b$.
关于以上两个结论,正确的判断是( )
| A. | ①成立,②不成立 | B. | ①不成立,②成立 | C. | ①成立,②成立 | D. | ①不成立,②不成立 |
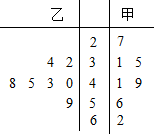 某餐饮连锁企业在某地级市东城区和西城区各有一个加盟店,两店在2015年的1~7月份的利润y(单位:万元)如茎叶图所示:
某餐饮连锁企业在某地级市东城区和西城区各有一个加盟店,两店在2015年的1~7月份的利润y(单位:万元)如茎叶图所示: