题目内容
证明：若集合M={（x，y）|x+y=0}，N={（x，y）|x2+y2=0}，则有M∪N=M．
考点：并集及其运算
专题：集合
分析：集合M中x与y互为相反数，集合N中x与y都为0，即可得证．
解答：
证明：由M中x+y=0，得到y=-x，即x与y互为相反数；
由N中x2+y2=0，得到x=0且y=0，
则M∪N=M．
由N中x2+y2=0，得到x=0且y=0，
则M∪N=M．
点评：此题考查了并集及其运算，熟练掌握并集的定义是解本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
函数y=sin（-x）（x∈[0，2π]）的简图是（ ）
A、 |
B、 |
C、 |
D、 |
等差数列{an}中，若a1=-11，a4+a6=-6，则公差d=（ ）
| A、4 | B、3 | C、2 | D、1 |
已知集合A={x|x＜3}，B={x|2＜x＜4}，则A∩B等于（ ）
| A、{x|x＜3} |
| B、{x|x＜4} |
| C、{x|2＜x＜3} |
| D、{x|2＜x＜4} |
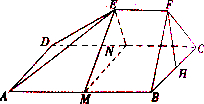如图，多面体EF-ABCD中，已知ABCD是边长为4的正方形，EF∥AB，平面FBC⊥平面ABCD，EF=2．