题目内容
已知两个圆锥有公共底面,且两圆锥的顶点和底面的圆周都在同一个球面上.这两个圆锥中,体积较小者的高与体积较大者的高的比值为
,则体积较小的圆锥与球的体积之比为 .
| 1 |
| 3 |
考点:球的体积和表面积
专题:计算题,空间位置关系与距离
分析:设体积较小者的高为h,体积较大者的高为3h,圆锥的底面半径为r,则r2=h•3h,可得r=
h,即可求出体积较小的圆锥与球的体积之比.
| 3 |
解答:
解:设体积较小者的高为h,体积较大者的高为3h,圆锥的底面半径为r,则r2=h•3h,
∴r=
h,
∴体积较小的圆锥与球的体积之比为
πr2h:
π•(2h)3=
.
故答案为:
.
∴r=
| 3 |
∴体积较小的圆锥与球的体积之比为
| 1 |
| 3 |
| 4 |
| 3 |
| 3 |
| 8 |
故答案为:
| 3 |
| 8 |
点评:本题是基础题,考查旋转体的体积,球的内接圆锥的体积的计算,考查计算能力,空间想象能力,常考题型.

练习册系列答案
相关题目
已知集合A={x|x<3},B={x|2<x<4},则A∩B等于( )
| A、{x|x<3} |
| B、{x|x<4} |
| C、{x|2<x<3} |
| D、{x|2<x<4} |
在某项测量中,测量结果ξ服从正态分布N(0,σ2)(σ>0),若P(ξ<-1)=0.1,则ξ在区间(0,1)内取值的概率为( )
| A、0.4 | B、0.5 |
| C、0.8 | D、0.9 |
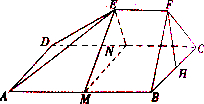 如图,多面体EF-ABCD中,已知ABCD是边长为4的正方形,EF∥AB,平面FBC⊥平面ABCD,EF=2.
如图,多面体EF-ABCD中,已知ABCD是边长为4的正方形,EF∥AB,平面FBC⊥平面ABCD,EF=2.