题目内容
已知数列{an}满足a1=1,an+1-an=
,则an=( )
| 1 | ||||
|
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:数列递推式
专题:点列、递归数列与数学归纳法
分析:由题意得an+1-an=
=
-
,利用累加法可得an的通项公式,
| 1 | ||||
|
| n+1 |
| n |
解答:
解:∵an+1-an=
=
-
∴an-an-1=
-
,
∴a2-a1=
-1,
a3-a2=
-
,
a4-a3=
-
,
…
∴an-an-1=
-
,
两边累加法得,
an-a1=
-1,
∵a1=1,
∴an=
,
故选:A
| 1 | ||||
|
| n+1 |
| n |
∴an-an-1=
| n |
| n-1 |
∴a2-a1=
| 2 |
a3-a2=
| 3 |
| 2 |
a4-a3=
| 4 |
| 3 |
…
∴an-an-1=
| n |
| n-1 |
两边累加法得,
an-a1=
| n |
∵a1=1,
∴an=
| n |
故选:A
点评:本题考查数列的性质和应用,解题时要认真审题,仔细解答.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
已知cos(
+α)=-
,且α为第四象限角,则cos(-3π+α)=( )
| 3π |
| 2 |
| 3 |
| 5 |
A、
| ||
B、-
| ||
C、±
| ||
D、
|
设M=
,N=
,P=
,Q
,则M与N、P与Q的大小关系为( )
| 102012+1 |
| 102013+1 |
| 102013+1 |
| 102014+1 |
| 102012+9 |
| 102013+100 |
| 102013+9 |
| 102014+100 |
| A、M>N,P<Q |
| B、M>N,P<Q |
| C、M>N,P<Q |
| D、M>N,P<Q |
下列说法错误的是( )
| A、在统计里,把所需考察对象的全体叫作总体 |
| B、平均数、众数与中位数从不同的角度描述了一组数据的集中趋势 |
| C、一组数据的平均数一定大于这组数据中的每个数据 |
| D、一组数据的方差越大,说明这组数据的波动越大 |
 在正方体ABCD-A1B1C1D1中,E,F,G,H分别为CC1,C1D1,DD1,CD的中点,N为BC的中点,试在E,F,G,H四个点中找两个点,使这两个点与点N确定一个平面α,且平面α∥平面BB1D1D.
在正方体ABCD-A1B1C1D1中,E,F,G,H分别为CC1,C1D1,DD1,CD的中点,N为BC的中点,试在E,F,G,H四个点中找两个点,使这两个点与点N确定一个平面α,且平面α∥平面BB1D1D.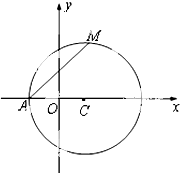 如图,已知圆C:(x-1)2+y2=r2(r>1),设A为圆C与x轴负半轴的交点,过点A作圆C的弦AM,并使弦AM的中点恰好落在y轴上.
如图,已知圆C:(x-1)2+y2=r2(r>1),设A为圆C与x轴负半轴的交点,过点A作圆C的弦AM,并使弦AM的中点恰好落在y轴上.