题目内容

在正方体ABCD-A1B1C1D1中，E，F，G，H分别为CC1，C1D1，DD1，CD的中点，N为BC的中点，试在E，F，G，H四个点中找两个点，使这两个点与点N确定一个平面α，且平面α∥平面BB1D1D．
考点：平面与平面平行的判定
专题：空间位置关系与距离
分析：如图所示，取FH，连接FN，HN，FH．由三角形的中位线定理可得NH∥BD，可得NH∥平面BB1D1D．由于四边形DHFD1是平行四边形，可得FH∥DD1，FH∥平面BB1D1D．即可证明．
解答： 解：如图所示，取FH，连接FN，HN，FH．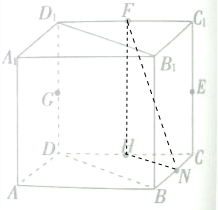
由三角形的中位线定理可得NH∥BD，
∵BD?平面BB1D1D，NH?平面BB1D1D．
∴NH∥平面BB1D1D．
由于四边形DHFD1是平行四边形，
∴FH∥DD1，
可得FH∥平面BB1D1D．
又NH∩FH=H．
∴平面FNH∥平面BB1D1D．
即α∥平面BB1D1D．
点评：本题考查了线面面面平行的判定定理、三角形的中位线定理、平行四边形的性质，考查了推理能力，属于基础题．
练习册系列答案
相关题目
已知sinx，cosx是方程x2-ax+
1
2
=0的两根，且π＜α＜
3π
2
，求
tan(3π-α)cos(π+α)-cos(-π+α)
sin(
π
2
+α)+cos(
π
2
-α)
的值．
已知函数f（x）=log4（4x+1）+kx（x∈R）的图象关于y轴对称．
（1）求k的值；
（2）若函数y=f（x）的图象与直线y=
1
2
x+b没有交点，求实数b的取值范围．
（3）设g（x）=log4（a•2x-a•m），当m取任意正数时，是否存在实数a，使得函数f（x）与 g（x）的图象有且只有一个公共点？若存在，求实数a的取值范围；若不存在，请说明理由．
已知函数f（x）=x2+
a-1
x
．
（1）讨论函数f（x）的奇偶性（不用证明）；
（2）在区间（2，+∞）上是增函数，求a的取值范围．
已知数列{an}满足a1=1，an+1-an=
1
n+1
+
n
，则an=（　　）
A、
n
B、
n+1
C、
1
n
D、
1
n+1
已知cos（
3π
2
-α）=
1
3
，sin（α+β）=1，求cos（2α+β）的值．
定义运算：
.
a1a2
b1 b2
.
=a1b2-a2b1，将函数f(x)=
.
sin2x-1
cos2x
3
.
的图象向左平移t（t＞0）个单位，所得图象对应的函数为奇函数，则t的最小值为（　　）
A、
π
6
B、
5
12
π
C、
π
3
D、
5π
6
（1）过点P（0，1）作直线l使它被直线l1：2x+y-8=0和l2：x-3y+10=0截得的线段被点P平分，求直线l的方程．
（2）已知过抛物线y2=2px（p＞0）的焦点斜率为2
2
的直线交抛物线于A（x1，y1）、B（x2，y2）（x1＜x2）两点，且|AB|=9，求该抛物线的方程．
已知3，x，12成等比数列，则正数x的值为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网