题目内容
在数列{an}中,若
=k(k为常数)则称 {an}为“等差比数列”.下列是对“等差比数列”的判断:
①k不可能为0;
②等差数列一定是等差比数列;
③等比数列一定是等差比数列;
④等差比数列中可以有无穷多项为0.
其中判断正确的个数为( )
| an+2-an+1 |
| an+1-an |
①k不可能为0;
②等差数列一定是等差比数列;
③等比数列一定是等差比数列;
④等差比数列中可以有无穷多项为0.
其中判断正确的个数为( )
| A、1个 | B、2个 | C、3个 | D、4个 |
考点:命题的真假判断与应用
专题:新定义
分析:当k=0时,则数列成了常数列,则分母也为0,进而推断出k不可能为0,判断出①正确.当等差数列和等比数列为常数列时不满足题设的条件,排除②③;对④,可令k=-1,举特例,进而推断④正确.
解答:
解:若公差比k为0,则an+2-an+1=0,故{an}为常数列,从而分母为0,无意义,所以公差比k一定不为零,故①正确.
当等差数列为常数列时不满足题设的条件,故②不正确.
当等比数列为常数列时,不满足题设,故③不正确.
对于④等差比数列中可以有无数项为0,比如k=-1,{an}:0,1,0,1,0,1…故④正确.
故选:B
当等差数列为常数列时不满足题设的条件,故②不正确.
当等比数列为常数列时,不满足题设,故③不正确.
对于④等差比数列中可以有无数项为0,比如k=-1,{an}:0,1,0,1,0,1…故④正确.
故选:B
点评:本题考查新定义,解题时应正确理解新定义,同时注意利用列举法、举反例判断命题为假.本题是一道中档题.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目
记等差数列{an}的前n项和为Sn,已知S7=28,S8=36,则S15=( )
| A、210 | B、120 |
| C、64 | D、56 |
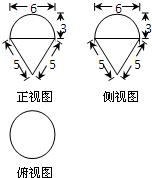 一个几何体的三视图如图所示,它的体积为( )
一个几何体的三视图如图所示,它的体积为( )| A、24π | B、30π |
| C、48π | D、72π |
若
=(1,2),
=(-3,m),
⊥
,则m=( )
| a |
| b |
| a |
| b |
A、
| ||
B、-
| ||
| C、6 | ||
| D、-6 |