题目内容
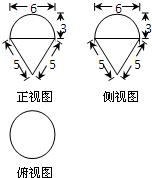一个几何体的三视图如图所示，它的体积为（ ）| A、24π | B、30π |
| C、48π | D、72π |
考点：由三视图求面积、体积
专题：计算题,空间位置关系与距离
分析：由三视图知几何体为半球与圆锥的组合体，且半球的半径为3，圆锥的母线长为5，底面圆的半径为3，把数据代入圆锥与半球的体积公式计算．
解答：
解：由三视图知几何体为半球与圆锥的组合体，且半球的半径为3；
圆锥的母线长为5，底面圆的半径为3，
∴圆锥的高为
=4．
∴几何体的体积V=
×π×33+
×π×32×4=30π．
故选：B．
圆锥的母线长为5，底面圆的半径为3，
∴圆锥的高为
| 52-32 |
∴几何体的体积V=
| 2 |
| 3 |
| 1 |
| 3 |
故选：B．
点评：本题考查了由三视图求几何体的体积，由三视图判断几何体的形状及数据所对应的几何量是解答的关键．
练习册系列答案
尖子生新课堂课时作业系列答案
英才计划同步课时高效训练系列答案
相关题目
在数列{an}中，若
=k(k为常数）则称 {an}为“等差比数列”．下列是对“等差比数列”的判断：
①k不可能为0；
②等差数列一定是等差比数列；
③等比数列一定是等差比数列；
④等差比数列中可以有无穷多项为0．
其中判断正确的个数为（ ）
| an+2-an+1 |
| an+1-an |
①k不可能为0；
②等差数列一定是等差比数列；
③等比数列一定是等差比数列；
④等差比数列中可以有无穷多项为0．
其中判断正确的个数为（ ）
| A、1个 | B、2个 | C、3个 | D、4个 |
已知{x|x2-1=0}?A⊆{-1，0，1}，集合A的子集的个数是（ ）
| A、3 | B、4 | C、6 | D、8 |
等差数列{an}的公差d≠0，an∈R，前n项和为Sn，则对正整数m，下列四个结论中：
（1）Sm，S2m-Sm，S3m-S2m成等差数列，也可能成等比数列；
（2）Sm，S2m-Sm，S3m-S2m成等差数列，但不可能成等比数列；
（3）Sm，S2m，S3m可能成等比数列，但不可能成等差数列；
（4）Sm，S2m，S3m不可能成等比数列，也不可能成等差数列；
正确的是（ ）
（1）Sm，S2m-Sm，S3m-S2m成等差数列，也可能成等比数列；
（2）Sm，S2m-Sm，S3m-S2m成等差数列，但不可能成等比数列；
（3）Sm，S2m，S3m可能成等比数列，但不可能成等差数列；
（4）Sm，S2m，S3m不可能成等比数列，也不可能成等差数列；
正确的是（ ）
| A、（1）（3） |
| B、（1）（4） |
| C、（2）（3） |
| D、（2）（4） |
y=4sinx-cos2x的值域是（ ）
| A、[-5，5] |
| B、[-1，4] |
| C、[-3，2] |
| D、[-3，5] |