题目内容
设x，y满足线性约束条件
，若目标函数z=abx+y（a＞0，b＞0）的最大值为6，则a+b的最小值为 ．
|
考点：简单线性规划的应用
专题：数形结合法,不等式的解法及应用
分析：画出满足约束条件的可行域，再根据目标函数z=abx+y（a＞0，b＞0）的最大值为6，求出a，b的关系式，再利用基本不等式求出a+b的最小值．
解答：
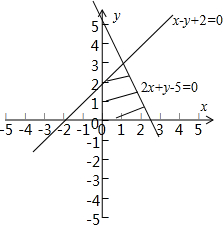解：满足线性约束条件
的区域是一个四边形，如图
4个顶点是（0，0），（0，2），（2.5，0），（1，3），
若目标函数在（1，3）取最大值6，
即6=ab+3，∴ab=3，
∴a+b≥2
=2
，当且仅当a=b时取等号，此时a+b的最小值为2
．
若目标函数在（2.5，0）取最大值6，即6=2.5ab，∴ab=
，
∴a+b≥2
=
，当且仅当a=b时取等号，此时a+b的最小值为
．
∴a+b的最小值为
．
故答案为：
．
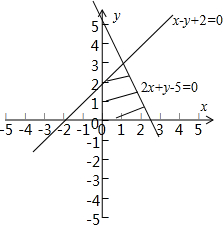解：满足线性约束条件
|
4个顶点是（0，0），（0，2），（2.5，0），（1，3），
若目标函数在（1，3）取最大值6，
即6=ab+3，∴ab=3，
∴a+b≥2
| ab |
| 3 |
| 3 |
若目标函数在（2.5，0）取最大值6，即6=2.5ab，∴ab=
| 12 |
| 5 |
∴a+b≥2
| ab |
4
| ||
| 5 |
4
| ||
| 5 |
∴a+b的最小值为
4
| ||
| 5 |
故答案为：
4
| ||
| 5 |
点评：本题考查线性规划知识的运用，用图解法解决线性规划问题时，分析题目的已知条件，找出约束条件和目标函数是关键．
练习册系列答案
阅读快车系列答案
相关题目
函数y=f（x）（x∈R）满足f（x-1）=f（x+1），且x∈[-1，1]时，f（x）=|x|，函数g（x）=
，则函数h（x）=f（x）-g（x）在区间[-5，5]上的零点个数为（ ）
|
| A、10 | B、9 | C、8 | D、7 |
已知点P（x，y）的坐标x，y满足
，则x2+y2-4x的取值范围是（ ）
|
| A、[0，12] |
| B、[-1，12] |
| C、[3，16] |
| D、[-1，16] |
已知函数f（x）=x2-4，点A1（x1，0），过点A1作x轴的垂线交抛物线C：y=f（x）于点B1，过B1作抛物线C：y=f（x）的切线与x轴交于点A2（x2，0），过点A2作x轴的垂线交抛物线C：y=f（x）于点B2，过点B2作抛物线C：y=f（x）的切线交x轴于点A3（x3，0）┉依次下去，得到x1、x2、x3┉，xn，其中x1＞0，函数y=x3-x2-x的单调递增区间为（ ）
A、(-∞，-
| ||
B、[-
| ||
C、(-∞，-
| ||
D、[-1，
|
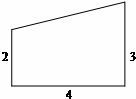在一张直角三角形纸片的两直角边上各取一点，分别沿斜边中点与这两点的连线剪去两个三角形，剩下的部分是如图所示的直角 梯形，其中三边长分别为2、4、3，则原直角三角形纸片的斜边长是