题目内容
函数y=f(x)(x∈R)满足f(x-1)=f(x+1),且x∈[-1,1]时,f(x)=|x|,函数g(x)=
,则函数h(x)=f(x)-g(x)在区间[-5,5]上的零点个数为( )
|
| A、10 | B、9 | C、8 | D、7 |
考点:正弦函数的图象,根的存在性及根的个数判断
专题:函数的性质及应用,三角函数的图像与性质
分析:由f(x-1)=f(x+1),得足f(x+2)=f(x),即函数f(x)是周期为2的周期函数,由h(x)=f(x)-g(x)=0得f(x)=g(x),分别作出函数f(x)与g(x)的图象,利用数形结合即可判断函数零点的个数.
解答:
解:∵f(x-1)=f(x+1),
∴f(x+2)=f(x),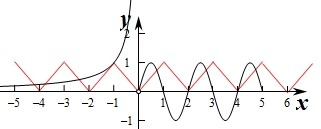
即函数f(x)是周期为2的周期函数,
由h(x)=f(x)-g(x)=0,
得f(x)=g(x),
∵x∈[-1,1]时,f(x)=|x|,函数g(x)=
,
∴分别作出函数f(x)与g(x)的图象,
由图象可知两个函数在区间[-5,5]上的交点个数为9个,
即函数h(x)=f(x)-g(x)在区间[-5,5]上的零点个数为9个.
故选:B
∴f(x+2)=f(x),

即函数f(x)是周期为2的周期函数,
由h(x)=f(x)-g(x)=0,
得f(x)=g(x),
∵x∈[-1,1]时,f(x)=|x|,函数g(x)=
|
∴分别作出函数f(x)与g(x)的图象,
由图象可知两个函数在区间[-5,5]上的交点个数为9个,
即函数h(x)=f(x)-g(x)在区间[-5,5]上的零点个数为9个.
故选:B
点评:本题主要考查方程根的个数的判断,利用方程和函数之间的关系,转化为两个函数图象的交点问题是解决本题的关键,利用数形结合是解决本题的基本思想.

练习册系列答案
相关题目
圆心为(1,2),半径为1的圆的标准方程为( )
| A、x2+(y-2)2=1 |
| B、x2+(y+2)2=1 |
| C、(x-1)2+(y-2)2=1 |
| D、(x+1)2+(y+2)2=1 |
 执行如图的程序框图,若输入x的值依次是:93,58,86,88,94,75,67,89,55,53,则输出m的值为( )
执行如图的程序框图,若输入x的值依次是:93,58,86,88,94,75,67,89,55,53,则输出m的值为( )