Question

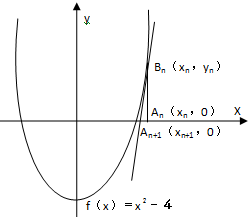
已知函数f（x）=x²-4，点A₁（x₁，0），过点A₁作x轴的垂线交抛物线C：y=f（x）于点B₁，过B₁作抛物线C：y=f（x）的切线与x轴交于点A₂（x₂，0），过点A₂作x轴的垂线交抛物线C：y=f（x）于点B₂，过点B₂作抛物线C：y=f（x）的切线交x轴于点A₃（x₃，0）┉依次下去，得到x₁、x₂、x₃┉，x_n，其中x₁＞0，
（1）求x_n+1与x_n的关系式；
（2）若x₁＞2，记an=lg

xn+2

xn-2

，证明数列{a_n}是等比数列；
（3）若x₁=

22

9

，求数列{na_n}的前n项和S_n．

Answer 1

考点：数列与解析几何的综合

专题：综合题,点列、递归数列与数学归纳法

分析：（1）求出原函数的导函数，写出切线L的方程，取y=0求得x的值，从而得到x_n+1与x_n的关系式；
（2）把a_n+1用x_n+1表示，结合x_n+1与x_n的关系得到a_n+1与a_n的关系，由关系证出数列{a_n}是等比数列；
（3）把x₁=

22

9

代入a1=lg

x1+2

x1-2

求出a₁，由等比数列求出通项公式，然后利用错位相减法求数列{na_n}的前n项和S_n．

解答： （1）解：∵f（x）=x²-4，
∴f′（x）=2x，
∴切线L的方程为y-(xn2-4)=2xn(x-xn)，
令y=0，得x=

xn

2

+

2

xn

，
即xn+1=

xn

2

+

2

xn

；

（2）证明：∵

xn+1+2

xn+1-2

=

xn 2 + 2 xn +2

xn 2 + 2 xn -2

=

xn2+4+4xn

xn2+4-4xn

=

(xn+2)2

(xn-2)2

，
∴an+1=lg

xn+1+2

xn+1-2

=2lg

xn+2

xn-2

=2an，
∴数列{a_n}是首项为a₁公比为2的等比数列；
（3）∵x₁=

22

9

，
∴a₁=lg

x1+2

x1-2

=lg

22 9 +2

22 9 -2

=lg10=1，
∴an=2n-1．
∴S_n=1×2⁰+2×2¹+3×2²+…+n×2^n-1
2S_n=1×2¹+2×2²+…+（n-1）×2ⁿ+n×2ⁿ
两式作差得：-S_n=1×2⁰+1×2¹+1×2²+…+1×2^n-1-n×2ⁿ=2ⁿ-1-n×2ⁿ．
∴S_n=n×2ⁿ+1-2ⁿ．

点评：本题考查了数列与解析几何的综合，考查了数列递推式，训练了利用错位相减法求数列的和，属中高档题．