题目内容

椭圆
x2
9
+
y2
25
=1的焦点坐标为（　　）
A、（-3，0），（3，0）
B、（-4，0），（4，0）
C、（0，-4），（0，4）
D、（0，-3），（0，3）
考点：椭圆的标准方程
专题：计算题,圆锥曲线的定义、性质与方程
分析：求出椭圆的a，b，由a2-b2=c2，计算即可得到焦点坐标．
解答： 解：椭圆
x2
9
+
y2
25
=1的a=5，b=3，
c=
a2-b2
=4，
则焦点为（0，-4），（0，4）．
故选：C．
点评：本题考查椭圆的方程和性质，考查椭圆的a，b，c的关系，考查运算能力，属于基础题．
练习册系列答案
相关题目
设有一个边长为3的正三角形，记为A1，将A1的每边三等份，在中间的线段上向图形外作正三角形，去掉中间的线段后所得到的图形记为A2；将A2的每边三等份，再重复上述过程，得到图形A3；再重复上述过程，得到图形A4，则A4的周长是（　　）
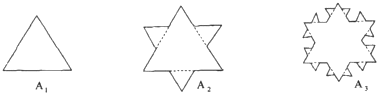
A、12
B、16
C、
64
3
D、
256
9
对定义在[0，1]上，并且同时满足以下两个条件的函数f（x）称为不等函数．
①对任意的x∈[0，1]，总有f（x）≥0；
②当x1≥0，x2≥0，x1+x2≤1时，总有f（x1+x2）≥f（x1）+f（x2）成立．
已知函数g（x）=x3与h（x）=2x-a是定义在[0，1]上的函数．
（1）试问函数g（x）是否为不等函数？并说明理由；
（2）若函数h（x）是不等函数，求实数a组成的集合．
已知点P在直线P1P2上，且
P1P
=
2
5
PP2
，若P1，P2，P的坐标分别为（x，-4，3），（-2，y，1），（3，0，z），求x，y，z．
一个球的体积是
32
3
π，这个球的半径等于（　　）
A、
1
2
B、1
C、2
D、2π
直线l：y=k（x+2）+4与曲线C：y=1+
4-x2
有两个交点，则k的取值范围
 
．
已知坐标平面上一点M（x，y）与两个定点M1（26，1），M2（2，1），且
|MM1|
|MM2|
=5．
（Ⅰ）求点M的轨迹方程，并说明轨迹是什么图形；
（Ⅱ）记（Ⅰ）中的轨迹为C，过点M（-2，3）的直线l被C所截得的线段的长为8，求直线l的方程．
若函数f（x）=x3+ax2+3x-9在x=-1时取得极值，则a等于（　　）
A、1B、2C、3D、4
函数y=sin（2x+
π
3
）的图象经下列怎样的平移后所得的图象关于点（-
π
12
，0）中心对称（　　）
A、向左平移
π
12
B、向右平移
π
12
C、向左平移
π
6
D、向右平移
π
6

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网