题目内容
直线l:y=k(x+2)+4与曲线C:y=1+
有两个交点,则k的取值范围 .
| 4-x2 |
考点:直线与圆的位置关系
专题:直线与圆
分析:根据直线过定点,以及直线和圆的位置关系即可得到结论.利用数形结合作出图象进行研究即可.
解答:
解:由y=k(x+2)+4知直线l过定点G(-2,4),由y=1+
,得y-1=
,两边平方得x2+(y-1)2=4,
则曲线是以(0,1)为圆心,2为半径,且位于直线y=1上方的半圆.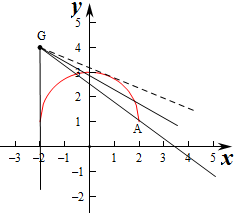
当直线过点A(2,1)时,直线l与曲线有两个不同的交点,
此时4k+4=1,
解得k=-
,
当直线l与曲线相切时,直线和圆有一个交点,
圆心(0,1)到直线kx-y+4+2k=0的距离d=
=2,
平方得k=-
,
要使直线y=kx+4+2k与曲线y=1+
有两个交点,
则直线l夹在两条直线之间,
因此-
≤k<-
,
故答案为:-
≤k<-
| 4-x2 |
| 4-x2 |
则曲线是以(0,1)为圆心,2为半径,且位于直线y=1上方的半圆.

当直线过点A(2,1)时,直线l与曲线有两个不同的交点,
此时4k+4=1,
解得k=-
| 3 |
| 4 |
当直线l与曲线相切时,直线和圆有一个交点,
圆心(0,1)到直线kx-y+4+2k=0的距离d=
| |2k+3| | ||
|
平方得k=-
| 5 |
| 12 |
要使直线y=kx+4+2k与曲线y=1+
| 4-x2 |
则直线l夹在两条直线之间,
因此-
| 3 |
| 4 |
| 5 |
| 12 |
故答案为:-
| 3 |
| 4 |
| 5 |
| 12 |
点评:本题主要考查直线和圆的位置关系的应用,利用数形结合是解决本题的关键,考查学生的计算能力.

练习册系列答案
相关题目
已知底面边长为1,侧棱长为ABCD的正四棱柱的各顶点均在同一个球面上,则该球的体积为( )
A、
| ||
| B、4π | ||
C、
| ||
| D、2π |
椭圆
+
=1的焦点坐标为( )
| x2 |
| 9 |
| y2 |
| 25 |
| A、(-3,0),(3,0) |
| B、(-4,0),(4,0) |
| C、(0,-4),(0,4) |
| D、(0,-3),(0,3) |
已知平面向量
=(1,2),
=(-2,m),且
⊥
,则m=( )
| a |
| b |
| a |
| b |
| A、1 | B、4 | C、-4 | D、-1 |
 如图所示的程序框图,其作用是输入x的值,输出相应的y的值.
如图所示的程序框图,其作用是输入x的值,输出相应的y的值. 如图,在山顶铁塔上B处测得一点铁A的俯角为α,在塔底C处测得A处的俯角为β,若铁塔高为m米,则山高CD为
如图,在山顶铁塔上B处测得一点铁A的俯角为α,在塔底C处测得A处的俯角为β,若铁塔高为m米,则山高CD为