题目内容
已知函数f(x)是定义在R上的奇函数,当x>0时,f(x)满足:2f(x)+xf′(x)>x2,则f(x)在区间[-1,1]内( )
| A、没有零点 |
| B、恰有一个零点 |
| C、至少一个零点 |
| D、至多一个零点 |
考点:利用导数研究函数的单调性,函数零点的判定定理,导数的运算
专题:导数的综合应用
分析:可构造函数g(x)=x2f(x),利用导数判断其单调性,即可得出结论.
解答:
解:令g(x)=x2f(x),则g′(x)=x[2f(x)+xf′(x)],
∵当x>0时,f(x)满足:2f(x)+xf′(x)>x2,
∴xg′(x)=x[2f(x)+xf′(x)]>x3>0,
∴当x>0时,g(x)>g(0)=0,∴f(x)>0,
又∵函数f(x)是定义在R上的奇函数,
∴当x<0时,f(x)<0,
∴f(x)在区间[-1,1]内只有一个零点为x=0.
故选B.
∵当x>0时,f(x)满足:2f(x)+xf′(x)>x2,
∴xg′(x)=x[2f(x)+xf′(x)]>x3>0,
∴当x>0时,g(x)>g(0)=0,∴f(x)>0,
又∵函数f(x)是定义在R上的奇函数,
∴当x<0时,f(x)<0,
∴f(x)在区间[-1,1]内只有一个零点为x=0.
故选B.
点评:本题主要考查利用构造函数法判断函数零点的知识,合理的构造函数是解决问题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
下列函数中,满足“对任意x1,x2∈(0,+∞),当x1<x2时,都有f(x1)>f(x2)”的是( )
| A、f(x)=(x-1)2 | ||
B、f(x)=
| ||
| C、f(x)=ex | ||
| D、f(x)=lnx |
若2014a=
,2014b=3,则a+2b等于( )
| 2014 |
| 9 |
| A、0 | B、1 | C、2 | D、3 |
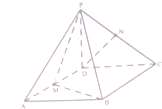 已知四棱锥P-ABCD,底面ABCD是∠A=60°,边长为a的菱形,又PD⊥底面ABCD,且PD=CD,点M,N分别是棱AD,PC的中点.
已知四棱锥P-ABCD,底面ABCD是∠A=60°,边长为a的菱形,又PD⊥底面ABCD,且PD=CD,点M,N分别是棱AD,PC的中点.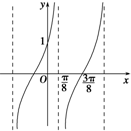 已知函数f(x)=Atan(ωx+ϕ)(
已知函数f(x)=Atan(ωx+ϕ)(