Question

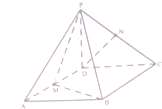已知四棱锥P-ABCD，底面ABCD是∠A=60°，边长为a的菱形，又PD⊥底面ABCD，且PD=CD，点M，N分别是棱AD，PC的中点．
（1）证明：DN∥平面PMB；
（2）证明：平面PMB⊥平面PAD；
（3）三棱锥A-PBM的体积．

Answer 1

考点：平面与平面垂直的判定,棱柱、棱锥、棱台的体积

专题：空间位置关系与距离

分析：（1）利用线面平行的判定定理进行判断．（2）利用面面垂直的判定定理进行判断．（3）V_A-PBM=V_P-ABM=

1

3

S_△ABM•PD，代入即可．

解答： 解：（1）证明：取PB中点Q，连结MQ、NQ，
因为M、N分别是棱AD、PC中点，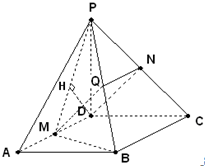
所以QN∥BC∥MD，且QN=MD，于是DN∥MQ．

DN∥MQ MQ⊆平面PMB DN?平面PMB

⇒DN∥平面PMB．
（2）

PD⊥平面ABCD MN⊆平面ABCD

⇒PD⊥MB，
又因为底面ABCD是∠A=60°，边长为a的菱形，且M为AD中点，
所以MB⊥AD．又AD∩PD=D，
所以MB⊥平面PAD．

MB⊥平面PAD MB⊆平面PMB

⇒平面PMB⊥平面PAD，
（3）V_A-PBM=V_P-ABM=

1

3

S_△ABM•PD=

1

3

•

1

2

•

a

2

•

3 a

2

•a=

3 a3

24

．

点评：本题主要考查直线和平面平行以及面面垂直的判定定理，要求熟练掌握相应的判定定理和应用．