题目内容
已知函数f(x)=sin(2x+
)-
cos(2x+
)+4sin2x,x∈R.
(Ⅰ)求函数f(x)的最小正周期;
(Ⅱ)求函数f(x)在区间[-
,
]上的值域.
| π |
| 3 |
| 3 |
| π |
| 3 |
(Ⅰ)求函数f(x)的最小正周期;
(Ⅱ)求函数f(x)在区间[-
| π |
| 4 |
| π |
| 4 |
考点:三角函数中的恒等变换应用,三角函数的周期性及其求法
专题:三角函数的求值,三角函数的图像与性质
分析:(Ⅰ)f(x)=sin(2x+
)-
cos(2x+
)+4sin2x通过恒等变换转化成:f(x)=2
sin(2x-
)+2,
进一步求出最小正周期
(Ⅱ)先根据x∈[-
,
],得2x-
∈[-
,
]进一步求出函数的值域.
| π |
| 3 |
| 3 |
| π |
| 3 |
| 2 |
| π |
| 4 |
进一步求出最小正周期
(Ⅱ)先根据x∈[-
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
| π |
| 4 |
解答:
解:(Ⅰ)f(x)=f(x)=sin(2x+
)-
cos(2x+
)+4sin2x
=2sin(2x+
-
)-2cos2x+2=2
sin(2x-
)+2,
所以T=π
(Ⅱ)由x∈[-
,
],得2x-
∈[-
,
]
当2x-
=-
,即x=-
时,函数有最小值2-2
当2x-
=
,即x=
时,函数有最大值4.
所以,f(x)∈[2-2
,4]
| π |
| 3 |
| 3 |
| π |
| 3 |
=2sin(2x+
| π |
| 3 |
| π |
| 3 |
| 2 |
| π |
| 4 |
所以T=π
(Ⅱ)由x∈[-
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
| π |
| 4 |
当2x-
| π |
| 4 |
| π |
| 2 |
| π |
| 8 |
| 2 |
当2x-
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
所以,f(x)∈[2-2
| 2 |
点评:本题考查的知识要点:三角函数的恒等变换,正弦型函数的周期,根据定义域求正弦型函数的值域.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
集合A={x∈N|-4<x-1<4,且x≠1}的真子集的个数为( )
| A、32 | B、31 | C、16 | D、15. |
已知集合A={x|x2+3x+2≥0},集合B={y|y=1-2x,x≤1},则∁AB=( )
| A、(-∞,-2] |
| B、(-∞,-2]∪[1,+∞) |
| C、(-∞,-1) |
| D、(-∞,-1)∪[1,+∞) |
已知函数f(x)是定义在R上的奇函数,当x>0时,f(x)满足:2f(x)+xf′(x)>x2,则f(x)在区间[-1,1]内( )
| A、没有零点 |
| B、恰有一个零点 |
| C、至少一个零点 |
| D、至多一个零点 |
设f(x)=2a2x-1,g(x)=x2+ax-1,若f(1)=g(1)且a≠1,则2a÷a2=( )
A、±2
| ||||
B、±
| ||||
C、2
| ||||
D、
|
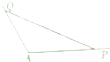 如图,角A为钝角,且sinA=
如图,角A为钝角,且sinA=