题目内容

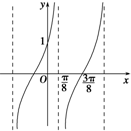已知函数f（x）=Atan（ωx+ϕ）（ω＞0，|ϕ|＜
π
2
）的部分图象如图，则f(
5π
24
)=
 
．
考点：由y=Asin（ωx+φ）的部分图象确定其解析式
专题：三角函数的图像与性质
分析：由正切型函数的图象得到其周期，由周期公式求得ω，结合函数图象过点（
3π
8
，0），（0，1）求得φ与A的值，则函数解析式可求，代入x=
5π
24
得答案．
解答： 解：由题意可知T=
π
2
，∴ω=2，
函数的解析式为：f（x）=Atan（ωx+φ），
∵函数过（
3π
8
，0），
∴0=Atan（
3π
4
+φ），
∴φ=
π
4
，
图象经过（0，1），
∴1=Atan
π
4
，则A=1，
∴f（x）=tan（2x+
π
4
），
则f(
5π
24
)=tan（
5π
12
+
π
4
）=-
3
．
故答案为：-
3
．
点评：本题考查了正切函数的图象和性质，解答此题的关键是正确求出函数周期，是基础题．
练习册系列答案
相关题目
已知集合A={x|（x-1）（x+2）＞0}，B={x|2-3x≤0}，C={y|y=x2}，求：
①A∪C；
②（∁UA）∩B．
已知函数f（x）是定义在R上的奇函数，当x＞0时，f（x）满足：2f（x）+xf′（x）＞x2，则f（x）在区间[-1，1]内（　　）
A、没有零点
B、恰有一个零点
C、至少一个零点
D、至多一个零点
设f（x）=2a2x-1，g（x）=x2+ax-1，若f（1）=g（1）且a≠1，则2a÷a2=（　　）
A、±2
2
B、±
2
2
C、2
2
D、
2
2
已知函数f(x)=
a
3
x3-
a+1
2
x2+x+b，其中a，b∈R．
（1）若曲线y=f（x）在点P（2，f（2））处的切线方程为y=5x-4，求f（x）的解析式；
（2）当函数f（x）在x=2处取得极值为
1
3
时，试确定f（x）在区间[
1
2
，3]上的最值．
若关于x的方程sin x+2|sin x|=k在x∈[0，2π]内有且仅有两个不同的实数解，则实数k的取值范围是
 
．
函数f（x）=x3-x+1的零点所在区间是（　　）
A、（-3，-2）
B、（-2，-1）
C、（-1，0）
D、（0，1）
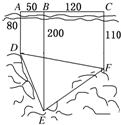如图，为了解某海域海底构造，在海平面内一条直线上的A，B，C三点进行测量，已知AB=50m，BC=120m，于A处测得水深AD=80m，于B处测得水深BE=200m，于C处测得水深CF=110m，则∠DEF的余弦值为（　　）
A、
16
65
B、
19
65
C、
16
57
D、
17
57
函数f（x）=（
1
2
） x2+2(a-1)x+2在区间（-∞，4]上单调递增，那么实数a的取值范围是（　　）
A、a≤-3B、a≥-3
C、a≤5D、a≥5

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网