题目内容
△ABC中，已知：sinA：sinB：sinC=1：1：
，且S△ABC=
，则
•
+
•
+
•
的值是（ ）
| 2 |
| 1 |
| 2 |
| AB |
| BC |
| BC |
| CA |
| AB |
| CA |
| A、2 | ||
B、
| ||
| C、-2 | ||
D、-
|
考点：平面向量数量积的运算
专题：解三角形,平面向量及应用
分析：先根据解三角形的有关知识，求出∴△ABC为等腰直角三角形，∠C=90°，∠B=∠A=45°，a=b=1，c=
，再根据向量的数量积求的结果
| 2 |
解答：
解：∵sinA：sinB：sinC=1：1：
=a：b：c，
设a=m，则，b=m，c=
m，
∵a2+b2=c2，
∴△ABC为等腰直角三角形，∠C=90°，∠B=∠A=45°
∵S△ABC=
，
∴
m2=
，
即m=1．
故a=b=1，c=
，
∴
•
+
•
+
•
=-
×1×cos45°-1×1×cos90°-1×1
cos45°=-2，
故选：C
| 2 |
设a=m，则，b=m，c=
| 2 |
∵a2+b2=c2，
∴△ABC为等腰直角三角形，∠C=90°，∠B=∠A=45°
∵S△ABC=
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
即m=1．
故a=b=1，c=
| 2 |
∴
| AB |
| BC |
| BC |
| CA |
| CA |
| AB |
| 2 |
| 2 |
故选：C
点评：本题考查了三角形的有关知识，以及勾股定理，向量的数量积的运算，属于中档题
练习册系列答案
阅读快车系列答案
相关题目
如图，在△ABC中，AB=BC=4，∠ABC=30°，AD是边BC 上的高，则| AD |
| AC |
| A、2 | B、4 | C、6 | D、8 |
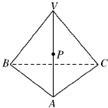一正四面体木块如图所示，点P是棱VA的中点，过点P将木块锯开，使截面平行于棱VB和AC，若木块的棱长为a，则截面面积为（ ）A、
| ||
B、
| ||
C、
| ||
D、
|