题目内容
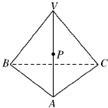 一正四面体木块如图所示,点P是棱VA的中点,过点P将木块锯开,使截面平行于棱VB和AC,若木块的棱长为a,则截面面积为( )
一正四面体木块如图所示,点P是棱VA的中点,过点P将木块锯开,使截面平行于棱VB和AC,若木块的棱长为a,则截面面积为( )A、
| ||
B、
| ||
C、
| ||
D、
|
考点:平面的基本性质及推论
专题:空间位置关系与距离
分析:利用线面平行的判定定理可以四边形PDEF为所求的截面,易知四边形PDEF为边长为
a的正方形,问题得以解决
| 1 |
| 2 |
解答:
 解:在平面VAC内作直线PD∥AC,交VC于D,
解:在平面VAC内作直线PD∥AC,交VC于D,
在平面VBA内作直线PF∥VB,交AB于F,
过点D作直线DE∥AC,交BC于E,
∵PF∥DE,
∴P,D,E,F四点共面,且面PDEF与VB和AC度平行,
易知四边形PDEF为边长为
a的正方形,
故其面积为
故选:C
 解:在平面VAC内作直线PD∥AC,交VC于D,
解:在平面VAC内作直线PD∥AC,交VC于D,在平面VBA内作直线PF∥VB,交AB于F,
过点D作直线DE∥AC,交BC于E,
∵PF∥DE,
∴P,D,E,F四点共面,且面PDEF与VB和AC度平行,
易知四边形PDEF为边长为
| 1 |
| 2 |
故其面积为
| a2 |
| 4 |
故选:C
点评:本题主要考查线面平行的判定和实际应用,关键之作出截面,属于基础题

练习册系列答案
相关题目
已知函数f(x)=x3-2x2-4x-7,其导函数为f′(x).
①f(x)的单调减区间是(
,2);
②f(x)的极小值是-15;
③当a>2时,对任意的x>2且x≠a,恒有f(x)>f(a)+f′(a)(x-a);
④函数f(x)有且只有一个零点.
其中真命题的个数为( )
①f(x)的单调减区间是(
| 2 |
| 3 |
②f(x)的极小值是-15;
③当a>2时,对任意的x>2且x≠a,恒有f(x)>f(a)+f′(a)(x-a);
④函数f(x)有且只有一个零点.
其中真命题的个数为( )
| A、1个 | B、2个 | C、3个 | D、4个 |
已知抛物线y2=ax(a>0),直线l过焦点F且与x轴不重合,则抛物线被l垂直平分的弦( )
| A、不存在 | B、有且仅有一条 |
| C、有2条 | D、有3条 |
定义在R上的函数f(x)满足f(x+6)=f(x).当-3≤x<-1时,f(x)=-(x+2)2,当-1≤x<3时,f(x)=x.则f(1)+f(2)+…+f(2014)=( )
| A、335 | B、336 |
| C、337 | D、2014 |
设点A是抛物线y2=4x上一点,点B(1.0),点M是线段AB的中点,若|AB|=3,则M 到直线x=-1的距离为( )
| A、5 | ||
B、
| ||
| C、2 | ||
D、
|
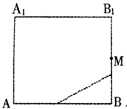
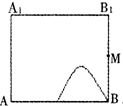
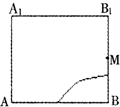
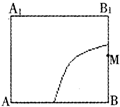
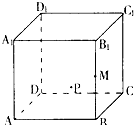 如图所示,在正方体ABCD-A1B1C1D1的侧面AB1内有一动点P到平面A1C1的距离是直线BC的距离的2倍,点M是棱BB1的中点,则动点P所在曲线的大致形状为( )
如图所示,在正方体ABCD-A1B1C1D1的侧面AB1内有一动点P到平面A1C1的距离是直线BC的距离的2倍,点M是棱BB1的中点,则动点P所在曲线的大致形状为( )