题目内容
已知直线y=
x与椭圆在第一象限交于M点,又MF2⊥x轴,F2是椭圆右焦点,另一个焦点为F1,若
•
=2,求椭圆的标准方程.
| ||
| 2 |
| MF1 |
| MF2 |
考点:椭圆的标准方程
专题:圆锥曲线的定义、性质与方程
分析:根据题意知道,焦点在x轴上,设出标准方程,再得到M的坐标,根据数量积,求出c的值,再根据点M在椭圆上,和椭圆的性质,求出a2,b2的值,问题得以解决
解答:
解:∵MF2⊥x轴,F2是椭圆右焦点,另一个焦点为F1,
∴焦点在x轴上,
可设椭圆方程为:
+
=1,(a>b>0),设焦点F2是的坐标为(c,0),F1是的坐标为(-c,0),
∵直线y=
x与椭圆在第一象限交于M点,
∴点M的坐标为(c,
c),
∴
=(-2c,-
c),
=(0,
c),
∵
•
=2,
∴
c2=2,
∴c=2,
∴点M的坐标为(2,
),
∵点M在椭圆上,
∴
+
=1,
∵a2=b2+c2,
∴a2=8,b2=4,
故椭圆的标准方程为
+
=1
∴焦点在x轴上,
可设椭圆方程为:
| x2 |
| a2 |
| y2 |
| b2 |
∵直线y=
| ||
| 2 |
∴点M的坐标为(c,
| ||
| 2 |
∴
| MF1 |
| ||
| 2 |
| MF2 |
| ||
| 2 |
∵
| MF1 |
| MF2 |
∴
| 1 |
| 2 |
∴c=2,
∴点M的坐标为(2,
| 2 |
∵点M在椭圆上,
∴
| 4 |
| a2 |
| 2 |
| b2 |
∵a2=b2+c2,
∴a2=8,b2=4,
故椭圆的标准方程为
| x2 |
| a2 |
| y2 |
| b2 |
点评:本题考查了椭圆的定义和性质,以及向量的数量积的运算,属于基础题

练习册系列答案
相关题目
定义在R上的函数f(x)满足f(x+6)=f(x).当-3≤x<-1时,f(x)=-(x+2)2,当-1≤x<3时,f(x)=x.则f(1)+f(2)+…+f(2014)=( )
| A、335 | B、336 |
| C、337 | D、2014 |
 如图,线段AB夹在一个直二面角的两个半平面内,它与两个半平面所成角都是30°,则AB与这个二面角的棱l所成角为( )
如图,线段AB夹在一个直二面角的两个半平面内,它与两个半平面所成角都是30°,则AB与这个二面角的棱l所成角为( )| A、30° | B、45° |
| C、60° | D、90° |
如果一个三位正整数的中间一个数字比另两个数字小,如305,414,879等,则称这个三位数为凹数,那么所有凹数的个数是( )
| A、240 | B、285 |
| C、729 | D、920 |
设点A是抛物线y2=4x上一点,点B(1.0),点M是线段AB的中点,若|AB|=3,则M 到直线x=-1的距离为( )
| A、5 | ||
B、
| ||
| C、2 | ||
D、
|
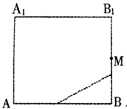
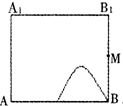
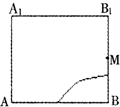
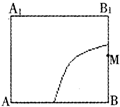
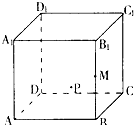 如图所示,在正方体ABCD-A1B1C1D1的侧面AB1内有一动点P到平面A1C1的距离是直线BC的距离的2倍,点M是棱BB1的中点,则动点P所在曲线的大致形状为( )
如图所示,在正方体ABCD-A1B1C1D1的侧面AB1内有一动点P到平面A1C1的距离是直线BC的距离的2倍,点M是棱BB1的中点,则动点P所在曲线的大致形状为( )