题目内容
13.已知抛物线C:y2=2px(p>0)过点A(1,-2).(1)求抛物线C的方程,并求其准线方程;
(2)若平行于OA(O为坐标原点)的直线l与抛物线C相交于M、N两点,且|MN|=3$\sqrt{5}$.求△AMN的面积.
分析 (1)点的坐标代入方程求出p即可得到抛物线方程.然后求解准线方程.
(2)设出直线方程,联立直线与抛物线方程,利用韦达定理以及弦长公式求出t,求出点到直线的距离,然后求解三角形面积.
解答 (10分)解:(1)将(1,-2)代入y2=2px,得(-2)2=2p•1,所以p=2.
故抛物线方程为y2=4x,准线为x=-1.…(3分)
(2)设直线l的方程为y=-2x+t,
由$\left\{\begin{array}{l}{y=-2x+t}\\{{y}^{2}=4x}\end{array}\right.$,得y2+2y-2t=0.∴y1+y2=-2,y1y2=-2t,…(5分).
∵直线l与抛物线C有公共点,∴△=4+8t≥0,解得t≥-$\frac{1}{2}$.
由|MN|=$\sqrt{1+\frac{1}{2}}\sqrt{4+8t}$=3$\sqrt{5}$得t=4,…(8分)
又A到直线l的距离为d=$\frac{4}{{\sqrt{5}}}$…(9分)
∴△AMN的面积为S=$\frac{1}{2}$|MN|﹒d=6.…(10分)
点评 本题考查抛物线与直线的位置关系的综合应用,抛物线的简单性质的应用,考查转化思想以及计算能力.

练习册系列答案
相关题目
3.设a,b,c,d是四条不同的直线,且a,b为异面直线,命题p“c与a,b都相交,d与a,b都相交”,命题q“c,d为相交直线”,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
1.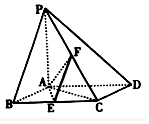 如图,已知四棱锥P-ABCD,地面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点.
如图,已知四棱锥P-ABCD,地面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点.
(1)证明:AE⊥PD;
(Ⅱ)若AB=2,PA=2,求四面体P-AEF的体积.
 如图,已知四棱锥P-ABCD,地面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点.
如图,已知四棱锥P-ABCD,地面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点.(1)证明:AE⊥PD;
(Ⅱ)若AB=2,PA=2,求四面体P-AEF的体积.
18.已知三棱锥P-ABC的四个顶点P,A,B,C都在半径为R的同一个球面上,若PA,PB,PC两两相互垂直,且PA=1,PB=2,PC=3,则R等于( )
| A. | $\frac{{\sqrt{14}}}{2}$ | B. | $\sqrt{14}$ | C. | $\frac{{\sqrt{13}}}{2}$ | D. | $\sqrt{3}$ |
2.设函数$f(x)=\left\{\begin{array}{l}3x+1,x<1\\{2^{x+b}},x≥1\end{array}\right.$,若$f[f(\frac{2}{3})]=4$,则b=( )
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
3.已知$l_1^{\;}$∥α,$l_2^{\;}?α$,则直线$l_1^{\;}$与$l_2^{\;}$的位置关系是( )
| A. | 平行或异面 | B. | 异面 | C. | 相交 | D. | 以上都不对 |