题目内容
1.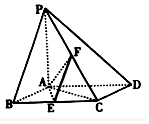 如图,已知四棱锥P-ABCD,地面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点.
如图,已知四棱锥P-ABCD,地面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点.(1)证明:AE⊥PD;
(Ⅱ)若AB=2,PA=2,求四面体P-AEF的体积.
分析 (I)通过证明AE⊥平面PAD得出AE⊥PD;
(II)连接PE,证明BC⊥平面PAE,于是VP-AEF=VF-PAE=$\frac{1}{2}$VC-PAE.
解答 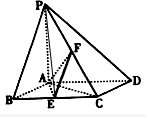 证明:(I)∵底面ABCD是菱形,∠ABC=60°,
证明:(I)∵底面ABCD是菱形,∠ABC=60°,
∴△ABC是等边三角形,
∵E是BC的中点,
∴AE⊥BC,又BC∥AD,
∴AE⊥AD,
∵PA⊥平面ABCD,AE?平面ABCD,
∴PA⊥AE,
又PA?平面PAD,AD?平面PAD,PA∩AD=A,
∴AE⊥平面PAD,又PD?平面PAD,
∴AE⊥PD.
(II)连接PE,
∵PA⊥平面ABCD,BC?平面ABCD,
∴PA⊥BC,又AE⊥BC,
∴BC⊥平面PAE,
∵四边形ABCD是菱形,AB=PA=2,∠ABC=60°,
∴AE=$\sqrt{3}$,
∴VC-PAE=$\frac{1}{3}$S△PAE•CE=$\frac{1}{3}×\frac{1}{2}×\sqrt{3}×2×1$=$\frac{\sqrt{3}}{3}$.
∵F是PC的中点,
∴VP-AEF=VF-PAE=$\frac{1}{2}$VC-PAE=$\frac{\sqrt{3}}{6}$.
点评 本题考查了线面垂直的判定与性质,棱锥的体积计算,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.若复数z1,z2在复平面内的对应点关于实轴对称,z1=2-i,则z1•z2=( )
| A. | -5 | B. | 5 | C. | -4+i | D. | -4-i |
6.下列说法正确的是( )
| A. | 直线的倾斜角的取值范围是[0°,180°] | |
| B. | 若直线的倾斜角为90°,则这条直线与y轴平行 | |
| C. | 任意一条直线都有倾斜角和斜率 | |
| D. | 若直线l的倾斜角为锐角,则它的斜率大于0;若直线l的倾斜角为钝角,则它的斜率小于0 |
11.已知集合A={x|x2+2x-3<0},B={x|log3x<1},则A∩B=( )
| A. | (0,1) | B. | (0,3) | C. | {-3,3} | D. | (1,4) |