题目内容
点P的极坐标为(
,
),那么它的直角坐标系表示为 .
| 2 |
| 3π |
| 4 |
考点:简单曲线的极坐标方程
专题:坐标系和参数方程
分析:由条件利用公式x=ρcosθ、y=ρsinθ,求得点P的直角坐标.
解答:
解:根据点P的极坐标为(
,
),可得 ρ=
、θ=
,
∴x=ρcosθ=-1,y=ρsinθ=1,故它的直角坐标系表示为 (-1,1),
故答案为:(-1,1).
| 2 |
| 3π |
| 4 |
| 2 |
| 3π |
| 4 |
∴x=ρcosθ=-1,y=ρsinθ=1,故它的直角坐标系表示为 (-1,1),
故答案为:(-1,1).
点评:本题主要考查把点的极坐标化为直角坐标的方法,利用了公式x=ρcosθ、y=ρsinθ,属于基础题.

练习册系列答案
相关题目
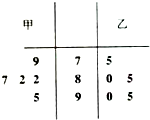 甲、乙两位同学参加数学竞赛培训,在培训期间,他们参加的5次预赛成绩数据茎叶图如图,下列对提供的数据分析正确的是( )
甲、乙两位同学参加数学竞赛培训,在培训期间,他们参加的5次预赛成绩数据茎叶图如图,下列对提供的数据分析正确的是( )A、
| ||||
B、
| ||||
| C、S甲2>S乙2 | ||||
| D、S甲2<S乙2 |
不等式(x-1)(x-2)<0的解集是( )
| A、(1,2) |
| B、(-∞,1)∪(2,+∞) |
| C、(-2,-1) |
| D、(-∞,-2)∪(-1,+∞) |
已知f(x)=x3-3x2+m,在区间[1,3]上任取三个数a,b,c,均存在以f(a),f(b),f(c)为边长的三角形,则m的取值范围是( )
| A、m>2 | B、m>4 |
| C、m>6 | D、m>8 |
阅读如图所示的程序框图,则输出的S的值为( )


A、-
| ||||
| B、0 | ||||
C、
| ||||
D、
|