题目内容
已知函数f(x)=
+
的最小值为m,最大值为M,则
的值为 .
| 2-x |
| x+2 |
| m |
| M |
考点:函数的最值及其几何意义
专题:计算题,函数的性质及应用
分析:根据解析式和根式有意义的条件,然后根据公式
≤
求出函数的最大值,然后再对y平方求出最小值,从而求解.
| a+b |
| 2 |
|
解答:
解:∵函数f(x)=
+
(-2≤x≤2),
∴f(x)=
+
≤2
=2
(当且仅当x=0时等号成立)
∴最大值为M=2
,
∵f2(x)=4+2
•
≥4(当x=-2或2时等号成立),
∴最小值为m=2,
则
=
=
,
故答案为:
.
| 2-x |
| x+2 |
∴f(x)=
| 2-x |
| x+2 |
|
| 2 |
∴最大值为M=2
| 2 |
∵f2(x)=4+2
| 2-x |
| x+2 |
∴最小值为m=2,
则
| m |
| M |
| 2 | ||
2
|
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:本题考查了函数的最值及其几何意义及公式
≤
的应用,是一道设计巧妙的好题.
| a+b |
| 2 |
|

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
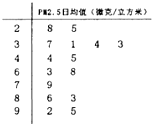 世卫组织规定,PM2.5日均值在35微克/立方米以下空气质量为一级;在35微克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.清远市环保局从市区2013年全年每天的PM2.5监测数据中随机抽取15天的数据作为样本,监测值如茎叶图所示(十位为茎,个位为叶),从这15天的数据中任取3天的数据,则恰有一天空气质量达到一级的概率为
世卫组织规定,PM2.5日均值在35微克/立方米以下空气质量为一级;在35微克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.清远市环保局从市区2013年全年每天的PM2.5监测数据中随机抽取15天的数据作为样本,监测值如茎叶图所示(十位为茎,个位为叶),从这15天的数据中任取3天的数据,则恰有一天空气质量达到一级的概率为