题目内容
已知f(x)=x3-3x2+m,在区间[1,3]上任取三个数a,b,c,均存在以f(a),f(b),f(c)为边长的三角形,则m的取值范围是( )
| A、m>2 | B、m>4 |
| C、m>6 | D、m>8 |
考点:利用导数求闭区间上函数的最值
专题:计算题,导数的综合应用
分析:三角形的边长为正数,而且任意两边之和大于第三边才能构成三角形,故只需求出函数在区间[1,3]上的最小值与最大值,从而可得不等式,即可求解.
解答:
解:由f′(x)=3x2-6x=3x(x-2)=0,得到x1=0(舍去),x2=2,
∵函数的定义域为[1,3],
∴函数在[1,2)上f′(x)<0,(2,3]上f′(x)>0,
∴函数f(x)在区间[1,2)单调递减,在区间(2,3]单调递增,
则f(x)min=f(2)=m-4,f(x)max=f(3)=m,f(1)=m-2,
由题意知,f(2)=m-4>0 ①;
f(2)+f(2)>f(3),即-8+2m>m②,
由①②得到m>8.
故选D.
∵函数的定义域为[1,3],
∴函数在[1,2)上f′(x)<0,(2,3]上f′(x)>0,
∴函数f(x)在区间[1,2)单调递减,在区间(2,3]单调递增,
则f(x)min=f(2)=m-4,f(x)max=f(3)=m,f(1)=m-2,
由题意知,f(2)=m-4>0 ①;
f(2)+f(2)>f(3),即-8+2m>m②,
由①②得到m>8.
故选D.
点评:本题以函数为载体,考查构成三角形的条件,解题的关键是求出函数在区间[1,3]上的最小值与最大值

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
为了解800名学生的学习情况,采用系统抽样的方法,从中抽取容量为40的样本,则分段的间隔为( )
| A、50 | B、40 | C、25 | D、20 |
i是虚数单位,若复数Z=i(1+3i),则复数Z的虚部是( )
| A、-3 | B、3i | C、1 | D、i |
要得到函数y=f′(x)的图象,需将函数f(x)=sinx-cosx(x∈R)的图象( )
A、向左平移
| ||
B、向右平移
| ||
| C、向左平移π个单位 | ||
| D、向右平移π个单位 |
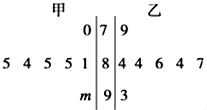 如图是某青年歌手大奖赛是七位评委为甲、乙两名选手打分的茎叶图(其中m是数字0~9中的一个),去掉一个最高分和一个最低分之后,甲、乙两名选手的方差分别是a1和a2,则( )
如图是某青年歌手大奖赛是七位评委为甲、乙两名选手打分的茎叶图(其中m是数字0~9中的一个),去掉一个最高分和一个最低分之后,甲、乙两名选手的方差分别是a1和a2,则( )| A、a1>a2 |
| B、a1<a2 |
| C、a1=a2 |
| D、a1,a2的大小与m的值有关 |
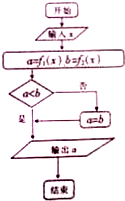 已知函数f1(x)=x,f2(x)=
已知函数f1(x)=x,f2(x)=