题目内容
已知数列{an}满足:a1=1,an+1-2an=n+1,n∈N*
(1)求证:数列{an+n+2}是等比数列;
(2)若数列{an}的前n项和为Sn,求an和Sn.
(1)求证:数列{an+n+2}是等比数列;
(2)若数列{an}的前n项和为Sn,求an和Sn.
考点:数列的求和,等比关系的确定
专题:等差数列与等比数列
分析:(1)由an+1-2an=n+1,n∈N*.变形为an+1+(n+3)=2(an+n+2),即可证明;
(2)由(1)可得an+n+2=4×2n-1=2n+1,可得an=2n+1-(n+2).再利用等差数列与等比数列的前n项和公式即可得出.
(2)由(1)可得an+n+2=4×2n-1=2n+1,可得an=2n+1-(n+2).再利用等差数列与等比数列的前n项和公式即可得出.
解答:
(1)证明:∵an+1-2an=n+1,n∈N*.
∴an+1+(n+3)=2(an+n+2),
a1+1+2=4,
∴数列{an+n+2}是等比数列,公比为2,首项为4;
(2)解:由(1)可得an+n+2=4×2n-1=2n+1,
∴an=2n+1-(n+2).
∴数列{an}的前n项和为Sn=
-
=2n+1-4-
n2-
n.
∴an+1+(n+3)=2(an+n+2),
a1+1+2=4,
∴数列{an+n+2}是等比数列,公比为2,首项为4;
(2)解:由(1)可得an+n+2=4×2n-1=2n+1,
∴an=2n+1-(n+2).
∴数列{an}的前n项和为Sn=
| 4(2n-1) |
| 2-1 |
| n(3+n+2) |
| 2 |
=2n+1-4-
| 1 |
| 2 |
| 5 |
| 2 |
点评:本题考查了等差数列与等比数列的通项公式及其前n项和公式,考查了变形能力,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
如图,阴影部分的面积是( )
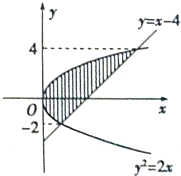

| A、16 | B、18 | C、20 | D、22 |
星光大道5位选手安排上场顺序,若选手A与选手B上场相邻,选手A与选手C上场不相邻,则不同的安排方案有( )
| A、36种 | B、48种 |
| C、72种 | D、120种 |
若a、b、c为实数,且a>b,则下面一定成立的是( )
| A、ac>bc |
| B、a2>b2 |
| C、a+c>b |
| D、a-c>b-c |