题目内容
若动圆O与直线4x+3y-7=0相切，且它的半径为4，则此动圆的圆心O的轨迹方程为 ．
考点：轨迹方程
专题：计算题,直线与圆
分析：设圆心坐标为（x，y），利用动圆O与直线4x+3y-7=0相切，且它的半径为4，建立方程，即可得出动圆的圆心O的轨迹方程．
解答：
解：设圆心坐标为（x，y），则
∵动圆O与直线4x+3y-7=0相切，且它的半径为4，
∴
=4，
∴4x+3y-7=±20，即4x+3y+13=0或4x+3y-27=0．
故答案为：4x+3y+13=0或4x+3y-27=0．
∵动圆O与直线4x+3y-7=0相切，且它的半径为4，
∴
| |4x+3y-7| | ||
|
∴4x+3y-7=±20，即4x+3y+13=0或4x+3y-27=0．
故答案为：4x+3y+13=0或4x+3y-27=0．
点评：本题考查求动圆的圆心O的轨迹方程，考查直线与圆的位置关系，比较基础．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知向量
=(2x，1)，向量
=(-4，2)，若
∥
，则
+
为（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| A、（-2，2） |
| B、（-6，3） |
| C、（2，-1） |
| D、（6，-3） |
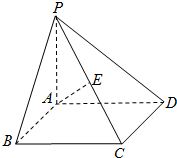如图，在四棱锥P-ABCD中，底面ABCD是矩形，PA⊥底面ABCD，E是PC的中点，已知PA=AB=2，AD=2已知集合A={-1，1}，B={x|ax=1}，若B⊆A，则a的取值集合为（ ）
| A、{1} |
| B、{-1} |
| C、{-1，1} |
| D、{-1，0，1} |