题目内容
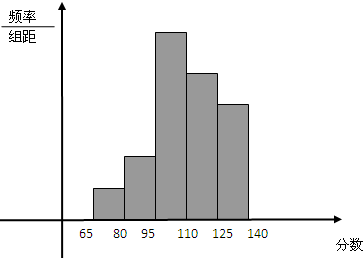
为了解某校高三模拟考生学生数学学习情况,从该校参加质检的学生数学成绩中抽出一个样本,并分成5组,绘成如图所示的频率分布直方图.若第二组至第五组数据的频率分别为 、 、 ,第一组数据的频数是 .
(1)估计该校高三学生质检数学成绩低于95分的概率,并求出样本容量;
(2)从样本中成绩在65分至95分之间的学生中任选两人,求至少有一人成绩在65至80分之间的概率.
(1)估计该校高三学生质检数学成绩低于95分的概率,并求出样本容量;
(2)从样本中成绩在65分至95分之间的学生中任选两人,求至少有一人成绩在65至80分之间的概率.

考点:列举法计算基本事件数及事件发生的概率,频率分布直方图
专题:概率与统计
分析:(1)求出样本中学生数学成绩低于95分频率和样本中第一组数据的频率,由此能求出该校高三学生质检数学成绩低于95分的概率,并求出样本容量.
(2)样本中成绩在65~80分之间的学生有2人,成绩在80~95分之间的学生有4人,由此利用列举法能求出至少有一人成绩在65至80分之间的概率.
(2)样本中成绩在65~80分之间的学生有2人,成绩在80~95分之间的学生有4人,由此利用列举法能求出至少有一人成绩在65至80分之间的概率.
解答:
解:(1)∵样本中学生数学成绩低于95分频率为1-0.4-0.3-0.15=0.15
∴该校高三模拟考试学生数学成绩低于95分概率为0.15,(2分)
又∵样本中第一组数据的频率为1-0.1-0.4-0.3-0.15=0.05,(4分)
∴样本容量为2÷0.05=40.(6分)
(2)样本中成绩在65~80分之间的学生有2人,记为x,y,
成绩在80~95分之间的学生40×0.1=4人,记为a,b,c,d,( 7分)
从上述6人中任选2人的所有可能情形有:{x,y},{x,a},{x,b},{x,c},{x,d},{y,a},
{y,b},{y,c},{y,d},{a,b},{a,c},{a,d},{b,c},{b,d},{c,d},共15种,(8分)
至少有1人在65~80分之间的可能情形有{x,y},{x,a},{x,b},{x,c},{x,d},{y,a},
{y,b},{y,c},{y,d},共9种,(11分)
因此,所求的概率为
=
. (12分)
∴该校高三模拟考试学生数学成绩低于95分概率为0.15,(2分)
又∵样本中第一组数据的频率为1-0.1-0.4-0.3-0.15=0.05,(4分)
∴样本容量为2÷0.05=40.(6分)
(2)样本中成绩在65~80分之间的学生有2人,记为x,y,
成绩在80~95分之间的学生40×0.1=4人,记为a,b,c,d,( 7分)
从上述6人中任选2人的所有可能情形有:{x,y},{x,a},{x,b},{x,c},{x,d},{y,a},
{y,b},{y,c},{y,d},{a,b},{a,c},{a,d},{b,c},{b,d},{c,d},共15种,(8分)
至少有1人在65~80分之间的可能情形有{x,y},{x,a},{x,b},{x,c},{x,d},{y,a},
{y,b},{y,c},{y,d},共9种,(11分)
因此,所求的概率为
| 9 |
| 15 |
| 3 |
| 5 |
点评:本题考查频率分布直方图的应用,考查概率的求法,是中档题,解题时要认真审题,注意列举法的合理运用.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
已知集合A={-1,1},B={x|ax=1},若B⊆A,则a的取值集合为( )
| A、{1} |
| B、{-1} |
| C、{-1,1} |
| D、{-1,0,1} |
某汽车销售公司经营年限x和销售总利润y(千万元),有以下的统计数据:
根据以上数据,求得线性回归方程
=
x+
中的
=0.85,由此可预测经营10年的销售总利润为( )
| x(年) | 2 | 3 | 4 | 5 | 6 |
| y(千万元) | 1.5 | 2 | 3 | 3.5 | 5 |
 |
| y |
 |
| b |
 |
| a |
 |
| b |
| A、7.25 | B、8.10 |
| C、8.90 | D、8.95 |
不等式组
的解集是( )
|
| A、(0,2) | ||
| B、(0,2.5) | ||
C、(0,
| ||
| D、(0,3) |
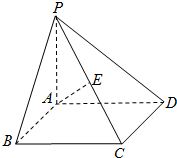 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,E是PC的中点,已知PA=AB=2,AD=2
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,E是PC的中点,已知PA=AB=2,AD=2