题目内容
已知不等式|x-3|+|x-4|≥m的解集为R,则实数m的取值范围( )
| A、m<1 | ||
| B、m≤1 | ||
C、m≤
| ||
D、m<
|
考点:函数恒成立问题
专题:函数的性质及应用,不等式的解法及应用
分析:根据绝对值不等式的解法和意义,即可得到结论.
解答:
解:要使不等式|x-3|+|x-4|≥m的解集为R,
则等价为(|x-3|+|x-4|)min≥m,
根据绝对值的几何意义,可知|x-3|+|x-4|表示数轴上的点x到3和4的距离之和的取值范围,
∴|x-3|+|x-4|≥1,
∴要使不等式|x-3|+|x-4|≥m的解集为R,
则m≤1,
故选:B.
则等价为(|x-3|+|x-4|)min≥m,
根据绝对值的几何意义,可知|x-3|+|x-4|表示数轴上的点x到3和4的距离之和的取值范围,
∴|x-3|+|x-4|≥1,
∴要使不等式|x-3|+|x-4|≥m的解集为R,
则m≤1,
故选:B.
点评:本题主要考查不等式恒成立,根据绝对值不等式的几何意义求出对应式子的最小值是解决本题的关键.

练习册系列答案
相关题目
已知幂函数y=x
(|p|、|q|是互质的整数)的图象如图所示,则p、q的关系为( )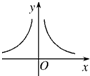
| p |
| q |

| A、pq>0,p、q均为奇数 |
| B、pq<0,p、q均为奇数 |
| C、pq<0,p为奇数,q为偶数 |
| D、pq<0,p为偶数,q为奇数 |
用数学归纳法证明“1+a+a2+…+a2n+1=
,(a≠1)”,在验证n=1时,左端计算所得项为( )
| 1-a2n+2 |
| 1-a |
| A、1+a+a2+a3+a4 |
| B、1+a |
| C、1+a+a2 |
| D、1+a+a2+a3 |
已知函数f(x)=ax2+2ax+1(-2<a<0),若x1<x2,且x1+x2=a,则( )
| A、f(x1)>f(x2) |
| B、f(x1)<f(x2) |
| C、f(x1)=f(x2) |
| D、f(x1),f(x2)大小不确定 |
| E、所以f(x1)>f(x2) |
若sin(
+α)=
,则sin2α等于( )
| π |
| 4 |
| 2 |
| 5 |
A、-
| ||
B、
| ||
C、-
| ||
D、
|
已知同心圆:x2+y2=25与x2+y2=9,若从外圆上一点做内圆的两条切线,则两条切线的夹角为( )
A、arctan
| ||
B、2arctan
| ||
C、π-arctan
| ||
D、π-2arctan
|