题目内容
已知函数f(x)=ax2+2ax+1(-2<a<0),若x1<x2,且x1+x2=a,则( )
| A、f(x1)>f(x2) |
| B、f(x1)<f(x2) |
| C、f(x1)=f(x2) |
| D、f(x1),f(x2)大小不确定 |
| E、所以f(x1)>f(x2) |
考点:二次函数的性质
专题:函数的性质及应用
分析:找到f(x)的对称轴x=-1,再考虑到
(x1+x2)在(-1,0),当
(x1+x2)=-1时,此时f(x1)=f(x2),再通过图象平移求得.
| 1 |
| 2 |
| 1 |
| 2 |
解答:
由函数表达式 f(x)=ax2+2ax+1=a(x+1)2+1-a 2,其对称轴为x=-1,又 x1+x2=a,所以-1<
(x1+x2)=
a<0,
当
(x1+x2)=-1时,此时f(x1)=f(x2),当图象向右移动时,所以f(x1)>f(x2)

| 1 |
| 2 |
| 1 |
| 2 |
当
| 1 |
| 2 |

点评:这个题中难题,考察二次函数的对称轴与区间的问题.

练习册系列答案
相关题目
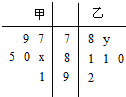 某学校从高二甲、乙两个班中各选6名同掌参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生成绩的众数是85,乙班学生成绩的平均分为81,则x+y的值为( )
某学校从高二甲、乙两个班中各选6名同掌参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生成绩的众数是85,乙班学生成绩的平均分为81,则x+y的值为( )| A、6 | B、7 | C、8 | D、9 |
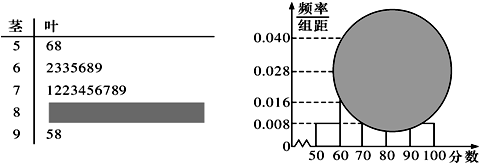
从某校高三数学学业水平测试卷中随机抽取部分试卷,对其成绩进行分析,因某特殊原因,所得的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如图,则频率分布直方图中,从左往右第四个矩形的面积为( )

A、
| ||
B、
| ||
C、
| ||
D、
|
已知n为正偶数,用数学归纳法证明1-
+
-
+…+
-
=2(
+
+…+
)时,第一步应验证( )
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n-1 |
| 1 |
| n |
| 1 |
| n+2 |
| 1 |
| n+4 |
| 1 |
| 2n |
A、1=2×
| ||||||||||
B、1-
| ||||||||||
C、1-
| ||||||||||
D、1-
|
等比数列{an}的各项为正数,且3是a5和a6的等比中项,则a1a2…a10=( )
| A、39 |
| B、310 |
| C、311 |
| D、312 |
已知不等式|x-3|+|x-4|≥m的解集为R,则实数m的取值范围( )
| A、m<1 | ||
| B、m≤1 | ||
C、m≤
| ||
D、m<
|
在等差数列{an}中,a1=-2012,其前n项和为Sn,若a12-a10=4,则S2012的值等于( )
| A、-2010 |
| B、-2011 |
| C、-2012 |
| D、-2013 |