题目内容
8.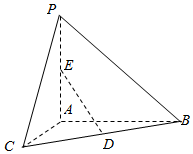 如图,已知PA⊥平面ABC,AC⊥AB,AP=BC,∠CBA=30°,D、E分别是BC、AP的中点,则异面直线AC与DE所成角的大小为$arccos\frac{{\sqrt{2}}}{4}$.
如图,已知PA⊥平面ABC,AC⊥AB,AP=BC,∠CBA=30°,D、E分别是BC、AP的中点,则异面直线AC与DE所成角的大小为$arccos\frac{{\sqrt{2}}}{4}$.
分析 取AB中点F,连接DF,EF,则AC∥DF,∠EDF就是异面直线AC与DE所成的角(或所成角的补角),由此能求出异面直线AC与ED所成的角的大小.
解答  解:取AB中点F,连接DF,EF,则AC∥DF,
解:取AB中点F,连接DF,EF,则AC∥DF,
∴∠EDF就是异面直线AC与DE所成的角(或所成角的补角).
设AP=BC=2,
∵PA⊥平面ABC,AC⊥AB,AP=BC,∠CBA=30°,D、E分别是BC、AP的中点,
∴由已知,AC=EA=AD=1,AB=$\sqrt{3}$,PB=$\sqrt{7}$,EF=$\frac{\sqrt{7}}{2}$,
∵AC⊥EF,∴DF⊥EF.
在Rt△EFD中,DF=$\frac{1}{2}AC=\frac{1}{2}$,DE=$\sqrt{2}$,
∴cos∠EDF=$\frac{D{E}^{2}+D{F}^{2}-E{F}^{2}}{2×DE×DF}$=$\frac{2+\frac{1}{4}-\frac{7}{4}}{2×\sqrt{2}×\frac{1}{2}}$=$\frac{\sqrt{2}}{4}$,
∴异面直线AC与ED所成的角为arccos$\frac{\sqrt{2}}{4}$.
故答案为:arccos$\frac{\sqrt{2}}{4}$.
点评 本题考查异面直线所成角的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
3.如图,正方体ABCD-A1B1C1D1中,棱长为1,点P在体对角线上,PB=$\frac{1}{3}$PB′,则P点坐标为( )
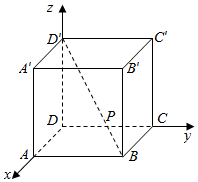

| A. | ($\frac{1}{3}$$,\frac{1}{3}$,$\frac{1}{3}$) | B. | ($\frac{2}{3}$,$\frac{2}{3}$,$\frac{2}{3}$) | C. | ($\frac{5}{6}$,$\frac{5}{6}$,$\frac{1}{6}$) | D. | ($\frac{2}{3}$,$\frac{2}{3}$,$\frac{1}{3}$) |
13.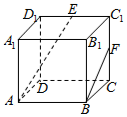 如图,在正方体ABCD-A1B1C1D1中,E,F分别是C1D1,CC1的中点,则异面直线AE与BF所成角的余弦值为( )
如图,在正方体ABCD-A1B1C1D1中,E,F分别是C1D1,CC1的中点,则异面直线AE与BF所成角的余弦值为( )
 如图,在正方体ABCD-A1B1C1D1中,E,F分别是C1D1,CC1的中点,则异面直线AE与BF所成角的余弦值为( )
如图,在正方体ABCD-A1B1C1D1中,E,F分别是C1D1,CC1的中点,则异面直线AE与BF所成角的余弦值为( )| A. | -$\frac{{5\sqrt{6}}}{18}$ | B. | -$\frac{{\sqrt{5}}}{5}$ | C. | $\frac{{\sqrt{6}}}{5}$ | D. | $\frac{{2\sqrt{5}}}{5}$ |


 如图,在四棱锥P-ABCD中,E,F,G分别是PB,AB,PC的中点,若四边形ABCD是平行四边形.求证:平面EFG∥平面PAD.
如图,在四棱锥P-ABCD中,E,F,G分别是PB,AB,PC的中点,若四边形ABCD是平行四边形.求证:平面EFG∥平面PAD.