题目内容
6．函数f（x）=ln$\frac{1}{（2-x）^{2}}$的大致图象是（ ）| A． |  | B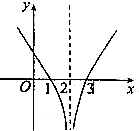． |  | C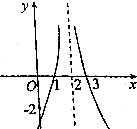． |  | D． |  |
分析 通过函数的定义域，以及函数的特殊点的坐标，判断求解即可．
解答 解：函数f（x）=ln$\frac{1}{（2-x）^{2}}$的定义域为：x≠2，函数的图象关于x=2对称，
x=0时，f（0）=ln$\frac{1}{4}$=-ln4＜0，所以图象A，B错误，
又ln4∈（1，2），所以C错误．
故选：D．
点评 本题考查函数的图象的应用，考查计算能力逻辑推理能力．
练习册系列答案
相关题目
16．已知θ为钝角，且sinθ+cosθ=$\frac{1}{5}$，则tan2θ=（ ）
| A． | -$\frac{24}{7}$ | B． | $\frac{24}{7}$ | C． | -$\frac{7}{24}$ | D． | $\frac{7}{24}$ |
17．已知x，y满足不等式组$\left\{\begin{array}{l}{x-y≤1}\\{x+2y≤2}\\{x≥1}\end{array}\right.$，且z=2x-y+a（a为常数）的最大值为2，则z的最小值为（ ）
| A． | $\frac{1}{2}$ | B． | -$\frac{1}{2}$ | C． | -$\frac{7}{6}$ | D． | $\frac{7}{6}$ |
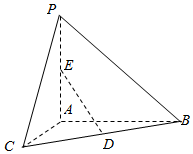如图，已知PA⊥平面ABC，AC⊥AB，AP=BC，∠CBA=30°，D、E分别是BC、AP的中点，则异面直线AC与DE所成角的大小为$arccos\frac{{\sqrt{2}}}{4}$．