题目内容

7．函数f（x）=$\sqrt{2-lo{g}_{2}x}$的定义域为（0，4]．

分析 由根式内部的代数式大于等于0，然后求解对数不等式得答案．

解答 解：由2-log2x≥0，得log2x≤2，解得0＜x≤4．
∴函数f（x）=$\sqrt{2-lo{g}_{2}x}$的定义域为（0，4]．
故答案为：（0，4]．

点评 本题考查函数的定义域及其求法，考查了对数不等式的解法，是基础题．

练习册系列答案
相关题目
17．已知x，y满足不等式组$\left\{\begin{array}{l}{x-y≤1}\\{x+2y≤2}\\{x≥1}\end{array}\right.$，且z=2x-y+a（a为常数）的最大值为2，则z的最小值为（　　）
A．$\frac{1}{2}$B．-$\frac{1}{2}$C．-$\frac{7}{6}$D．$\frac{7}{6}$
18．已知sin+θcosθ=$\frac{1}{2}$，0＜θ＜π，tan2θ=$\frac{3\sqrt{7}}{7}$．
15．已知向量$\overrightarrow{a}$，$\overrightarrow{b}$满足，|$\overrightarrow{a}$|=2，|$\overrightarrow{b}$|=5，$\overrightarrow{a}$•$\overrightarrow{b}$=6，λ∈R，则|$\overrightarrow{a}$-λ$\overrightarrow{b}$|的取值范围是[$\frac{8}{5}$，+∞）．
2．已知复数z=$\frac{10{i}^{2016}}{（3+i）^{2}}$，则在复平面内，复数z所对应的点位于（　　）
A．第一象限B．第二象限C．第三象限D．第四象限
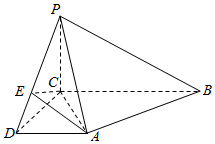4．等差数列{an}前n项和为Sn，且$\frac{{S}_{2016}}{2016}$=$\frac{{S}_{2015}}{2015}$+1，则数列{an}的公差为（　　）
A．1B．2C．2015D．2016
11．如图，在四棱锥P-ABCD中，AD∥BC，且BC=2AD，AD⊥CD，PB⊥CD，点E在棱PD上，且PE=2ED．
（1）求证：平面PCD⊥平面PBC；
（2）求证：PB∥平面AEC．
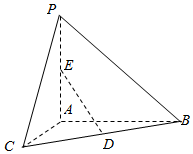8．如图，已知PA⊥平面ABC，AC⊥AB，AP=BC，∠CBA=30°，D、E分别是BC、AP的中点，则异面直线AC与DE所成角的大小为$arccos\frac{{\sqrt{2}}}{4}$．
9．已知圆C：（x-1）2+y2=r2（r＞0）与直线l：y=x+3，且直线l有唯一的一个点P，使得过P点作圆C的两条切线互相垂直，则r=2；设EF是直线l上的一条线段，若对于圆C上的任意一点Q，∠EQF≥$\frac{π}{2}$，则|EF|的最小值=4$\sqrt{2}$+2．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网