题目内容
20. 如图,在四棱锥P-ABCD中,E,F,G分别是PB,AB,PC的中点,若四边形ABCD是平行四边形.求证:平面EFG∥平面PAD.
如图,在四棱锥P-ABCD中,E,F,G分别是PB,AB,PC的中点,若四边形ABCD是平行四边形.求证:平面EFG∥平面PAD.
分析 由中位线定理得EF∥AP,EG∥BC∥AD,故而平面EFG∥平面PAD.
解答 证明:∵E,F,G分别是PB,AB,PC的中点,
∴EF∥PA,EG∥BC,
∵四边形ABCD是平行四边形,
∴BC∥AD,
∴EG∥AD,
又EF?平面EFG,EG?平面EFG,EF∩EG=E,AP?平面PAD,AD?平面PAD,AP∩AD=A,
∴平面EFG∥平面PAD.
点评 本题考查了面面平行的判定,属于基础题.

练习册系列答案
相关题目
15.已知a<-1<b<0<c<1,则下列不等式成立的是( )
| A. | b2<c<a2 | B. | ab+$\frac{1}{ab}$<c | C. | $\frac{1}{b}$<$\frac{1}{a}$<$\frac{1}{c}$ | D. | b2>ab-bc+ac |
5.在菱形ABCD中,A=60°,AB=2$\sqrt{3}$,将△ABD沿BD折起到△PBD的位置,若二面角P-BD-C的大小为120°,则三棱锥P-BCD的外接球体积为( )
| A. | $\frac{28\sqrt{7}}{3}$π | B. | 28$\sqrt{7}$π | C. | $\frac{32}{3}$π | D. | 4$\sqrt{3}$π |
10.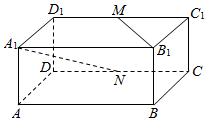 长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=1,M、N分别是C1D1、CD的中点,则异面直线A1N和B1M所成角的余弦值为( )
长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=1,M、N分别是C1D1、CD的中点,则异面直线A1N和B1M所成角的余弦值为( )
 长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=1,M、N分别是C1D1、CD的中点,则异面直线A1N和B1M所成角的余弦值为( )
长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=1,M、N分别是C1D1、CD的中点,则异面直线A1N和B1M所成角的余弦值为( )| A. | $\frac{\sqrt{30}}{10}$ | B. | 0 | C. | $\frac{\sqrt{15}}{10}$ | D. | $\frac{1}{6}$ |
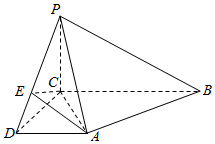 如图,在四棱锥P-ABCD中,AD∥BC,且BC=2AD,AD⊥CD,PB⊥CD,点E在棱PD上,且PE=2ED.
如图,在四棱锥P-ABCD中,AD∥BC,且BC=2AD,AD⊥CD,PB⊥CD,点E在棱PD上,且PE=2ED.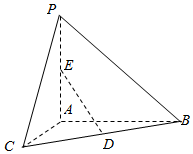 如图,已知PA⊥平面ABC,AC⊥AB,AP=BC,∠CBA=30°,D、E分别是BC、AP的中点,则异面直线AC与DE所成角的大小为$arccos\frac{{\sqrt{2}}}{4}$.
如图,已知PA⊥平面ABC,AC⊥AB,AP=BC,∠CBA=30°,D、E分别是BC、AP的中点,则异面直线AC与DE所成角的大小为$arccos\frac{{\sqrt{2}}}{4}$.