题目内容
16.函数$y=x\sqrt{1-{x^2}}({0<x<1})$的最大值为$\frac{1}{2}$.分析 根据基本不等式的性质求出函数的最大值即可.
解答 解:$y=x\sqrt{1-{x^2}}({0<x<1})$≤$\frac{{x}^{2}+1{-x}^{2}}{2}$=$\frac{1}{2}$,
当且仅当x=$\frac{\sqrt{2}}{2}$时“=”成立,
故$y=x\sqrt{1-{x^2}}({0<x<1})$的最大值为:$\frac{1}{2}$,
故答案为:$\frac{1}{2}$.
点评 本题考查了基本不等式的性质,考查转化思想,是一道基础题.

练习册系列答案
相关题目
4.等差数列{an}前n项和为Sn,且$\frac{{S}_{2016}}{2016}$=$\frac{{S}_{2015}}{2015}$+1,则数列{an}的公差为( )
| A. | 1 | B. | 2 | C. | 2015 | D. | 2016 |
5.在菱形ABCD中,A=60°,AB=2$\sqrt{3}$,将△ABD沿BD折起到△PBD的位置,若二面角P-BD-C的大小为120°,则三棱锥P-BCD的外接球体积为( )
| A. | $\frac{28\sqrt{7}}{3}$π | B. | 28$\sqrt{7}$π | C. | $\frac{32}{3}$π | D. | 4$\sqrt{3}$π |
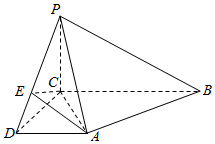 如图,在四棱锥P-ABCD中,AD∥BC,且BC=2AD,AD⊥CD,PB⊥CD,点E在棱PD上,且PE=2ED.
如图,在四棱锥P-ABCD中,AD∥BC,且BC=2AD,AD⊥CD,PB⊥CD,点E在棱PD上,且PE=2ED.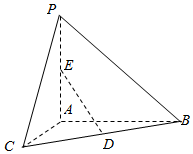 如图,已知PA⊥平面ABC,AC⊥AB,AP=BC,∠CBA=30°,D、E分别是BC、AP的中点,则异面直线AC与DE所成角的大小为$arccos\frac{{\sqrt{2}}}{4}$.
如图,已知PA⊥平面ABC,AC⊥AB,AP=BC,∠CBA=30°,D、E分别是BC、AP的中点,则异面直线AC与DE所成角的大小为$arccos\frac{{\sqrt{2}}}{4}$.