题目内容
3.如图,正方体ABCD-A1B1C1D1中,棱长为1,点P在体对角线上,PB=$\frac{1}{3}$PB′,则P点坐标为( )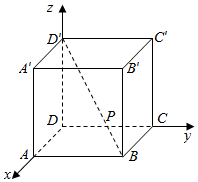
| A. | ($\frac{1}{3}$$,\frac{1}{3}$,$\frac{1}{3}$) | B. | ($\frac{2}{3}$,$\frac{2}{3}$,$\frac{2}{3}$) | C. | ($\frac{5}{6}$,$\frac{5}{6}$,$\frac{1}{6}$) | D. | ($\frac{2}{3}$,$\frac{2}{3}$,$\frac{1}{3}$) |
分析 根据题意,设出点P(x,y,z),结合题意利用坐标表示列出方程组,求出解即可.
解答 解:如图所示,
设点P(x,y,z),且点B(1,1,0),B′(1,1,1),D′(0,0,1);
∵点P在正方体ABCD-A1B1C1D1的对角线BD′,∴x=y①,
又PB=$\frac{1}{3}$PB′,
∴(x-1)2+(y-1)2+z2=$\frac{1}{9}$[(x-1)2+(y-1)2+(z-1)2]②,
又$\overrightarrow{PB}$与$\overrightarrow{BD′}$共线,∴$\frac{x-1}{-1}$=$\frac{y-1}{-1}$=$\frac{z}{1}$③;
由①②③组成方程组,解得$\left\{\begin{array}{l}{x=\frac{5}{6}}\\{y=\frac{5}{6}}\\{z=\frac{1}{6}}\end{array}\right.$;
∴P点坐标为($\frac{5}{6}$,$\frac{5}{6}$,$\frac{1}{6}$).
故选:C.
点评 本题考查了空间向量的坐标表示与运算问题,也考查了解方程组的应用问题,是基础题目.

练习册系列答案
相关题目
2.已知复数z=$\frac{10{i}^{2016}}{(3+i)^{2}}$,则在复平面内,复数z所对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
15.已知a<-1<b<0<c<1,则下列不等式成立的是( )
| A. | b2<c<a2 | B. | ab+$\frac{1}{ab}$<c | C. | $\frac{1}{b}$<$\frac{1}{a}$<$\frac{1}{c}$ | D. | b2>ab-bc+ac |
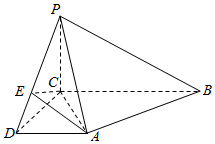 如图,在四棱锥P-ABCD中,AD∥BC,且BC=2AD,AD⊥CD,PB⊥CD,点E在棱PD上,且PE=2ED.
如图,在四棱锥P-ABCD中,AD∥BC,且BC=2AD,AD⊥CD,PB⊥CD,点E在棱PD上,且PE=2ED.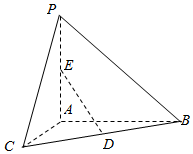 如图,已知PA⊥平面ABC,AC⊥AB,AP=BC,∠CBA=30°,D、E分别是BC、AP的中点,则异面直线AC与DE所成角的大小为$arccos\frac{{\sqrt{2}}}{4}$.
如图,已知PA⊥平面ABC,AC⊥AB,AP=BC,∠CBA=30°,D、E分别是BC、AP的中点,则异面直线AC与DE所成角的大小为$arccos\frac{{\sqrt{2}}}{4}$.