题目内容
在约束条件
下,若目标函数z=-2x+y的最大值不超过4,则实数m的取值范围( )
|
A、(-
| ||||
B、[0,
| ||||
C、[-
| ||||
D、[-
|
考点:简单线性规划
专题:不等式的解法及应用
分析:作出可行域,平移直线y=2x可知当直线经过点A(
,
)时,目标函数取最大值,由题意可得m的不等式,解不等式可得.
| 1-m2 |
| 2 |
| 1+m2 |
| 2 |
解答:
 解:作出约束条件
解:作出约束条件
所对应的可行域(如图阴影),
变形目标函数可得y=2x+z,解方程组
可得
平移直线y=2x可知当直线经过点A(
,
)时,目标函数取最大值,
∴-2×
+
≤4,解得-
≤m≤
,
∴实数m的取值范围为[-
,
]
故选:D
 解:作出约束条件
解:作出约束条件
|
变形目标函数可得y=2x+z,解方程组
|
|
平移直线y=2x可知当直线经过点A(
| 1-m2 |
| 2 |
| 1+m2 |
| 2 |
∴-2×
| 1-m2 |
| 2 |
| 1+m2 |
| 2 |
| 3 |
| 3 |
∴实数m的取值范围为[-
| 3 |
| 3 |
故选:D
点评:本题考查简单线性规划,涉及不等式的解法,准确作图是解决问题的关键,属中档题.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
等腰三角形ABC底边两端点是A(-
,0),B(
,0),顶点C的轨迹是( )
| 3 |
| 3 |
| A、一条直线 | B、一条直线去掉一点 |
| C、一个点 | D、两个点 |
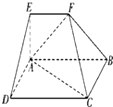 如图,在多面体ABCDEF中,四边形ABCD是矩形,AB∥EF,∠EAB=90°,AB=4,AD=AE=EF=1,平面ABEF⊥平面ABCD,则点D到平面BCF的距离为
如图,在多面体ABCDEF中,四边形ABCD是矩形,AB∥EF,∠EAB=90°,AB=4,AD=AE=EF=1,平面ABEF⊥平面ABCD,则点D到平面BCF的距离为